|
搬送波位相測定値による精密測位の理論及び解析処理 |
Home |
A.4.付 座標系の定義と変換
A.4. 付.1 地球固定座標系
A.4. 付.2 緯度・経度・高度
A.4. 付.3 局地座標系
A.4. 付.4 衛星固定座標系
A.4. 付.5 慣性座標系
本文で使われている座標系の定義とそれらの間の変換を以下にまとめる。
精密測位において一般に使用される座標系は地心地球固定座標系(ECEF:Earth Centered Earth Fixed)である。地心地球固定座標系は地球重心を原点にして北極方向をz軸、グリニッジ子午線面をx軸に、右手直交座標系を成すようy軸を定めた三次元直交座標系である。地球固定座標系のうち国際標準の基準座標系と呼べるのが国際地球回転事業(IERS:International Earth Rotation Service)が構築・維持している国際地球基準座標系(ITRF: International Terrestrial Reference Frame)である。ITRFの最新のものはITRF2000と呼ばれVLBI、SLR、GPS等の精密測地技術で決定した全世界の基準点の座標及び速度(座標変化率)により定義される。
なおGPSが準拠する基準座標系は厳密には米国が構築・維持している基準座標系であるWGS84だが現在はほぼITRFと同一のものと考えてよい。本文中及び以下では簡単のためこれらの標準的な地心地球固定座標系のことを単に地球固定座標系と呼ぶ。
これらの地球固定座標系で地球重心を原点として定義されるが例えばITRFの原点と瞬時の地球重心には僅かな差がありかつその値は時間変動していることが宇宙測地技術を使った精密な観測で分かってきた。この差をGeocenter Offsetと呼ぶが通常1cm未満の値であり無視することが多い。
観測点の緯度・経度を![]() ,
,![]() 、高度を
、高度を![]() (m)とすると地球固定座標系での観測点位置
(m)とすると地球固定座標系での観測点位置![]() (m)は以下で表すことができる。
(m)は以下で表すことができる。
![]()
![]()
![]()
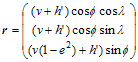
ここで![]() は楕円体高(m)である。
は楕円体高(m)である。![]() は緯度・経度
は緯度・経度![]() ,
,![]() におけるジオイド高(m)であり適当なジオイドモデルから求める。
におけるジオイド高(m)であり適当なジオイドモデルから求める。![]() ,
,![]() はそれぞれ地球赤道半径(m)及び地球扁平率でありジオイドモデルの準拠楕円体、一般にはGRS80またはWGS84で定義された値を使用する。図A.4.23に楕円体高、ジオイド高、高度の関係を示す。ここで厳密には鉛直線偏差の考慮が必要だが通常はその値は十分小さいので無視している。
はそれぞれ地球赤道半径(m)及び地球扁平率でありジオイドモデルの準拠楕円体、一般にはGRS80またはWGS84で定義された値を使用する。図A.4.23に楕円体高、ジオイド高、高度の関係を示す。ここで厳密には鉛直線偏差の考慮が必要だが通常はその値は十分小さいので無視している。
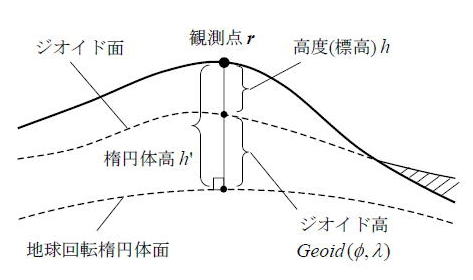
図 A.4.23 高度の関係
また逆に地球固定座標系での観測点の位置を![]() (m)として、観測点の緯度・経度
(m)として、観測点の緯度・経度![]() ,
,![]() 、高度
、高度![]() (m)は以下により求めることができる。
(m)は以下により求めることができる。
![]()
![]()
![]()
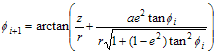
![]()
![]()
![]()
ここで緯度![]() は逐次近似計算により求める。
は逐次近似計算により求める。
観測点の位置を原点として東、北、上方向をそれぞれ![]() 軸とする三次元直交座標系を観測点の局地水平面座標系(Local
Tangent Coordinate)と呼ぶ。本文中及び以下では簡単のため観測点の局地水平面座標系のことを観測点の局地座標系と呼ぶ。観測点の緯度・経度を
軸とする三次元直交座標系を観測点の局地水平面座標系(Local
Tangent Coordinate)と呼ぶ。本文中及び以下では簡単のため観測点の局地水平面座標系のことを観測点の局地座標系と呼ぶ。観測点の緯度・経度を![]() ,
,![]() として地球固定座標系から観測点の局地座標系への座標系回転行列
として地球固定座標系から観測点の局地座標系への座標系回転行列![]() は以下で表される。
は以下で表される。
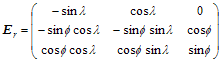
逆に観測点の局地座標系から地球固定座標系への座標系回転行列は![]() で表すことができる。
で表すことができる。
衛星固定座標系は衛星重心位置を原点に、送信アンテナ方向をz軸方向、太陽電池パドルの回転軸方向をy軸とし、右手直交座標系を成すようx軸を決めた衛星に固定された三次元直交座標系である。ただしここで、太陽方向がx軸の正の方向になる様その向きを決める。衛星固定座標系の定義を図A.4.24に示す。
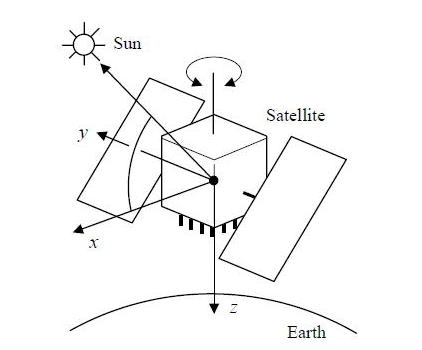
図 A.4.24 衛星固定座標系の定義(GPS)
地球固定座標系での衛星位置を![]() 、太陽位置を
、太陽位置を![]() として衛星固定座標系から地球固定座標系への座標系回転行列
として衛星固定座標系から地球固定座標系への座標系回転行列![]() は以下で与えられる。
は以下で与えられる。
![]() ,
, ![]() ,
, ![]()
![]()
![]()
なおこの変換は衛星がノミナルの姿勢すなわちアンテナ面を地心方向、太陽電池パドル面を太陽方向に向けているという仮定をおいている。従って食の場合等通常とは異なる姿勢制御モードにある場合正常な値を求めることができない。
衛星軌道決定などの際に地心慣性座標系 (ECI:Earth Centered Inertial)での取扱いが必要になる場合がある。地球固定座標系と地心慣性座標系の間の変換には、地球自転軸の方向や回転角を決定するために、精密な歳差・章動モデルや地球回転パラメータ(ERP:Earth Rotation Parameters)を使った複雑な計算が必要になる。詳細は/7/,/8/を参照のこと。通常の測位計算で地心慣性座標系を使うことは少ないのでここでは説明を省略する。
| A.4.7 おわりに← | →参照文献 |
| Copyright (C) 2005 by Tomoji Takasu, All rights reserved |