IGS P1-P2バイアス値(衛星) (2004/1/1-2004/12/31) (表示プログラム)
|
GPSによる精密単独測位(PPP)に関する覚え書き |
Return |
目次
・PPPの原理
・PPPと相対測位の比較
・軌道補間(1)
・軌道補間(2) 11/1追加
・時計補間
・幾何距離モデル
・座標変換補正
・時計推定
・擬似距離バイアス
・観測ノイズモデル
・測位モードによる時間感度の差
・Static PPPにおける局位置プロセスノイズパラメータ
・Clock Steeringに伴う擬似距離観測値の飛び
・サイクルスリップ編集(1)
・サイクルスリップ編集(2)
・サイクルスリップ編集(3)
・オンラインGPS精密解析サービス
・時計の定義(1) 11/1追加
精密単独測位(PPP)はGPS精密衛星軌道、時計推定値と搬送波観測データを使って基準局を使わずに精密測位を行う手法である。条件にもよるが一般的な二重位相差を使った相対測位とほぼ同等程度の測位精度が得られる。
.....................................................................................................................................
| 項目 | 精密単独測位(PPP) | 相対測位 | 備考 | |
|---|---|---|---|---|
| 基本観測量 | ゼロ差搬送波位相 | 二重位相差 | ||
| 使用衛星暦 | 精密暦(軌道・時計) | 精密暦(軌道)、放送暦 | ||
| 基準局 | 不要 | 必要 | ||
| 決定座標 | 世界測地系による絶対座標 | 基準局相対座標 (基線ベクトル) | ||
| 電離層遅延補正 | 2周波による補正 | 2周波補正(長基線)、補正なし(短基線) | ||
| 搬送波位相バイアス | 実数値推定 | 整数化による精度向上 | ||
| 測位精度 | kinematic | TBD | TBD | |
| 短期static | TBD | TBD | 1H | |
| 長期static | 水平3mm、垂直6mm | 水平3mm,垂直6mm+基線長×1ppb | 24H | |
| 応用分野 | グローバル・ローカル地殻変動計測 GPS気象学、時刻同期 |
一般測位 ローカル地殻変動計測 |
||
.....................................................................................................................................
軌道補間(1)
IGS精密暦の軌道は15分間隔の衛星位置しか与えられないので15分より短い間隔で推定を行う場合補間を行う必要がある。また衛星-観測局の幾何距離を求める際に衛星速度が必要になるため衛星位置から速度を推定する必要がある。これらの補間、速度推定精度は直接測位精度に影響を及ぼすため補間アルゴリズムが重要である。GTでは高精度の補間を行うため精密衛星運動モデルを使いて軌道補間を行っている。GTにおける軌道補間アルゴリズムは以下の通りである。
・衛星位置(地球固定座標)を歳差・章動モデルと地球回転パラメータにより慣性座標系に変換する。
・補間間隔毎に精密衛星運動モデルによる常微分方程式の2点境界値問題を解く。すなわち補間間隔両端の衛星位置を精密暦に一致させるよう先頭時刻の衛星速度を求める。
・2点境界値問題の解法としてはいわゆる狙い撃ち法を使っている。初期値としては最初の区間は位置と時刻差から算出した概算値、次区間以降は前区間の終点速度を使う。常微分方程式の数値解法としては固定ステップ4次Runge-Kuttaを使用している。
・精密衛星運動モデルとしては以下の摂動を考慮している:地球重力8次、月・太陽重力、太陽輻射圧モデルCODE(固定パラメータ)、食モデル=円筒モデル
・以上で求まった補間点の衛星位置及び速度(慣性座標)を再度、歳差・章動モデル及び地球回転パラメータにより地球固定座標に変換する。
以上の補間アルゴリズムの補間誤差は運動モデルの近似誤差が支配的であり概ねΔa*t2/2(Δa:加速度誤差)で求めることができる。GTの場合運動モデルの近似誤差は太陽輻射圧モデルの誤差で決まる。GPS衛星軌道において太陽輻射圧加速度は概ね10-7m/s2であり固定パラメータによる誤差を10%と見積もると加速度誤差はΔa=10-8m/sとなる。補間区間の中点で最も補間精度が悪くなるのでこの点での補間誤差は10-8m/s2×450s2/2=1mmとなる。この補間誤差は精密暦精度5cm以下に比べ十分小さいので無視できる。
なお以上のように精密運動モデルを使わない補間は全て補間誤差に伴う精度劣化が懸念される。
軌道補間について補足
GTでは運動モデルで補間する関係上、衛星位置はいったん慣性座標に変換し再度地球固定座標に戻している。以前はどうせ戻すのだからとこの座標変換時の地球回転パラメータを0に固定していたのだが、PPP時の残差を解析すると補間値使用epochの値が明らかに大きく精度を落としている事が確認できたので、現在はIERS
Bulletin Bを使っている。あと15分間隔で常微分方程式境界値問題を解いている関係で補間時間が結構かかる。29衛星1日分を30秒間隔に補間するのに約30分。従ってPPP時にはgeneph.mを使って事前に補間した軌道を使う必要がある。
軌道補間についての補足(2)
軌道補間については一般にはラグランジェ補間、スプライン補間等が使われることが多い。17次ラグランジェ補間でmm精度を達成可能との報告もある。これらの補間精度については今後評価予定である。
.....................................................................................................................................
精密暦の衛星軌道補間は一般にはラグランジェ補間等の多項式補間が使われることが多い。以下精密暦補間精度の評価を行った。
補間はn次ラグランジェ。ただし補間区間は補間点を中心としてn+1点を取る。例えば9次なら補間点を挟むように前後5点ずつ取って10点9次で補間する。補間次数を変えて評価した補間精度を以下に示す。ここでは精密衛星運動モデルを使った補間値と比較した誤差を示す。日替り近くの精度悪化を防ぐため当日だけでなく、前日、翌日の精密暦も同時に使用している。
| degree of polynomial |
Position Error (cm) | Velocity Error (cm/sec) | ||||||
|---|---|---|---|---|---|---|---|---|
| 3D | Radial | AlongTrk | CrossTrk | 3D | Radial | AlongTrk | CrossTrk | |
| n=5 | 118.12 | 72.10 | 73.84 | 57.48 | 0.415 | 0.253 | 0.260 | 0.202 |
| n=6 | 11.57 | 7.31 | 6.89 | 5.75 | 0.051 | 0.032 | 0.031 | 0.025 |
| n=7 | 1.02 | 0.63 | 0.63 | 0.50 | 0.029 | 0.017 | 0.019 | 0.014 |
| n=8 | 0.16 | 0.08 | 0.11 | 0.08 | 0.028 | 0.017 | 0.018 | 0.013 |
| n=9 | 0.13 | 0.05 | 0.11 | 0.05 | 0.028 | 0.017 | 0.018 | 0.013 |
| n=10 | 0.13 | 0.05 | 0.10 | 0.06 | 0.028 | 0.017 | 0.018 | 0.013 |
| n=11 | 0.14 | 0.05 | 0.12 | 0.06 | 0.028 | 0.017 | 0.018 | 0.013 |
| n=13 | 0.15 | 0.06 | 0.12 | 0.06 | 0.028 | 0.017 | 0.018 | 0.013 |
| n=15 | 0.15 | 0.06 | 0.13 | 0.06 | 0.028 | 0.017 | 0.018 | 0.013 |
n=10の際の衛星毎の補間誤差を以下に示す。大部分で誤差が2mm以下に収まっているが例えばPRN29の日替わり近くで1cmを超える誤差が出ている。この時期のPRN29はIGS精密暦作成時の運動モデル不整合が大きい衛星であり精密暦の値も少し怪しいので評価は難しい。
| PRN01 | PRN03 | PRN04 | PRN05 | PRN06 | PRN07 | PRN08 | PRN09 | PRN10 | PRN11 |
| PRN13 | PRN14 | PRN15 | PRN16 | PRN17 | PRN18 | PRN19 | PRN20 | PRN21 | PRN22 |
| PRN23 | PRN24 | PRN25 | PRN26 | PRN27 | PRN28 | PRN29 | PRN30 | PRN31 |
以上より軌道補間は概ね8次以上の多次多項式補間を使えばほぼ十分な精度が出ることが分かった。一部衛星で日替わり付近で1cmを超えることがあるがこれは精密暦の問題の可能性が高い。
なお以上は高度の高いGPS衛星では多項式補間で十分精度が出るということで他の軌道の衛星では状況が異なる。例えばLEO衛星であるGRACEはやってみると多次多項式補間では十分な精度は出ないようだ。これは空気抵抗や高次地球重力項が衛星運動に効いていて、多項式展開した場合の高次項の寄与を無視できないためであると考えられる。
.....................................................................................................................................
時計補間
IGS精密暦の時計は5分間間隔値が公開されている。時計安定度は通常Allan
Deviationと呼ぶ時間間隔τの関数σy(τ)で表され、Rayの論文によればτ=300sにおけるGPS衛星時計のAllan
Deviationは以下の通り。Block II/IIA 3×10-12(Cesium), 2×10-11(Rubidium), Block IIR 2×10-12〜5×10-13
精密暦時計を補間する場合補間中点でやはり最も精度が悪くなりその補間誤差は時計安定度で決まる。τ=150sのAllan
Deviationを上記論文グラフから外挿で求めると、Block II/IIA 1×10-11(Cesium), 8×10-11(Rubidium), Block IIR 3×10-12〜1×10-12。従って中点での補間誤差はBlock II/IIA 1.5ns(Cesium),
12ns(Rubidium), Block IIR 0.45ns〜0.15nsと見積もることができる。
これらの補間誤差は精密暦時計誤差0.1ns以下に比較し十分大きいので補間値を使うと精度劣化の可能性が高い。
現在、JPL及びCODE AC解の時計には30秒間隔の衛星時計推定値が含まれているので、30秒間隔解析の場合これを使うほうが良い。
なお30秒間隔時計の補間誤差を上と同様に見積もると、Block
II/IIA 3ns(Cesium), 15ns(Rubidium), Block
IIR 0.15ns、と5分間隔時計に比べ改善されない。
従って30秒未満間隔の高時間分解能PPPでは精密時計をどこから入手するかが問題となる。
その後衛星時計推定値を基に現在のGPS衛星に関して時計補間誤差を評価した。その結果、5分間隔時計補間誤差で0.1ns〜0.6ns、30秒間隔時計補間誤差で0.03〜0.06ns程度の精度が得られることがわかった。これらの誤差は精密暦時計誤差0.1ns以下に対し無視は出来ないが誤差を考慮して使用すれば十分使用可能であると考えられる。
.....................................................................................................................................
幾何距離モデル(1)
GPSによる高精度測位計算を行う際には衛星と局の位置から衛星-受信アンテナ間の幾何距離(Geometric
Distance)を精密に求める必要がある。 この距離を精密に求めるためには信号の伝播遅延を考慮した光路差方程式(Light-Time
Equation)と呼ぶ方程式を解かな ければならない。
この方程式では伝播遅延以外に信号伝播中の衛星及び局の慣性空間上での移動や受信機時計誤差を考慮する必要がある。
受信機時計誤差は衛星位置が通常GPS時刻系に同期して与えられる(あるいは推定する)のでその時刻系と信号受信時刻が
ずれている効果も補正するために必要である。
GTが使用している幾何距離モデルを以下に示す。
GPS衛星の場合、信号伝播遅延+受信機時計誤差Δtは高々0.1秒以下なのでこの間の衛星運動は簡易なモデルで近似しても
十分精度が出る。 GTではこの衛星運動は衛星・地球の二体問題の2次近似により解いている。
衛星速度が十分な精度で与えられると仮定して近似誤差は概ねΔa*Δt2/2で与えられ、この場合のΔaは地球重力 のJ2項が支配的でGPS軌道において10-4m/s2くらいの値のため、Δt=0.1sとして近似誤差は最大
0.0005mmであり無視できる。 static測位の場合、局の移動はほとんど地球の自転によるものであり、地球赤道半径Re=6378km、
自転速度ω=0.729×10-4rad/sとしてこの時間内の赤道上局の移動はReωΔtで与えられ50mくらいになる。
この程度の時間内では地球自転軸の方向は十分に安定なので、GTでは歳差・章動モデルと地球回転パラメータを使って
GPS時刻系に同期した時刻の自転軸を出し、その自転軸を中心とした回転運動で近似している。
なおこの幾何距離モデルについて著名なGPS解析ソフトであるBerneseは衛星運動の地球重力効果を無視している。
(Bernese5.0 Draft Document 2.3 Observation Equation参照) 地球重力による加速度はGPS軌道で1m/s2程度でありそれによる衛星位置の変化は0.1sで最大5mm程度になるので
、これを無視することにより測位精度劣化に結びつく可能性がある。
Berneseは実績のあるすばらしい精密解析ソフトだが使っているモデルが若干古いきらいがある。(この項続く)
.....................................................................................................................................
幾何距離モデル(2)
光路差方程式では式の両辺に幾何距離項ρが出てくるのでそのままでは解けない。従って数値計算の定法に従いiterationによりρを求める。この方程式は非常に収束が速くρ=0を初期値にしても通常3,4回で十分な精度でρを求めることが出来る。
衛星軌道及び局位置をパラメータ推定する際に必要となるので同時に幾何距離の衛星位置・速度による偏微分係数を求める。Δt=0の場合、幾何距離の衛星位置による偏微分係数は局から衛星を見た視線方向単位ベクトル、衛星速度による偏微分係数は0ベクトルとなる。それに衛星位置・速度のt-Δtからtへの状態遷移行列を掛けることによりΔt分の衛星位置・速度の変化分を補正する。GTではこの状態遷移行列も地球重力を考慮した衛星運動方程式の2次近似により求めている。
.....................................................................................................................................
座標変換補正
IGS Orbit/Clockを使ったPPPでは何も補正をしないと垂直15〜20mmの系統誤差が出る。GTではそのためIGS
ITRF局のPPP結果とITRF座標を使って最小二乗法でHelmert変換係数を求め座標変換補正を行い最終推定座標としている。(Helmert変換係数の推定)
IGS ITRF局PPP結果 (補正なし)、IGS ITRF局PPP結果(補正有り)
Helmert変換による補正係数のうち垂直座標の補正に効くのはほとんどScaleパラメータで大きさは大体2〜3ppbくらいの値である。IGSでは精密暦の品質監視のための継続的にPPPによりITRF局座標を決定しその結果を公開している。その結果を見てもほぼ同様の補正係数値が得られている。補正係数のうちdx,dy,dzはGeocenterオフセット、Rx,Ry,Rzは地球回転パラメータ誤差に起因するものと理解できるがScaleパラメータについては必ずしも原因が明瞭でない。ITRF系はGPSだけでなくVLBI,SLR等の他の測地手段も使って決定されているから、この補正項はGPS計測独自の特性に起因するものである可能性が高い。この原因としてひとつ考えられているのは解析に使用している衛星及び受信アンテナ位相中心オフセットの問題である。現在IGS解析センターで標準として使われている受信アンテナ位相中心オフセット/変動パラメータはIGS_01.PCVだがこのパラメータは特定のアンテナに対する相対値として計測され決定されたものである。また衛星アンテナ位相中心オフセットについては衛星Block毎に固定の値を使用しており必ずしも現実の値と合致していない可能性がある。IGSではこの問題に対応するため"absolute"アンテナ位相中心パラメータの導入を計画している様であり、将来的にはその導入によりScaleパラメータによる補正は必要なくなるかもしれない。
.....................................................................................................................................
時計推定
PPPにおいては衛星軌道及び時計を精密暦等に固定し局位置等を推定するが、この際使用する時計がどう算出されているかが重要である。良く知られているように2周波(L1,L2)の擬似距離間には主に衛星及び受信機の回路遅延差に伴うDCB(Differential
Code Bias)あるいはIFB(Inter-Frequency Bias)と呼ぶバイアスが存在する。また新しい型のコードレス受信機においてはL1搬送波についてC/Aコード(C1),P(Y)コード(P1)の2種類の擬似距離が計測できその間には同様にバイアスが存在する。通常時計は擬似距離を使って測るのでこれらのバイアスをどう扱うかで時計推定値が変わる。
結論から書くと現在のIGS ClockはP1及びP2擬似距離の電離層フリー線形結合を使って決定されている。P1の計測が出来ない受信機についてはP1の代わりにC1を後で説明するP1-C1バイアスで補正した値が使用される。なおこの手順はGPS
Week 1056 (200/04/02)から開始されておりそれ以前の時計推定値は異なった擬似距離を使って決定されているので注意が必要である。
以上よりP1擬似距離を計測できる2周波受信機とIGS
Clockを使ってPPP解析を行う場合、擬似距離バイアスを考慮する必要は無い。擬似距離バイアスを考慮する必要があるのは1周波観測の場合及びP1を計測できない受信機を使用する場合のみである。
さて、上で時計は擬似距離を使って測ると書いたがこれは厳密には正しくない。高精度の時計推定には擬似距離と搬送波位相の両者が使われる。すなわち時計の時間変動については搬送波位相、絶対値については擬似距離により測る。これは擬似距離には主にマルチパスによる大きな雑音成分が加わること及び搬送波位相のみでは搬送波位相バイアスと時計バイアスの分離が出来ないことによる。ここで擬似距離は推定期間中の平均値として時計バイアスの絶対値決定に使用される。擬似距離には主にマルチパスによるバイアス成分が含まれるがIGS
Clockの場合はマルチパスを含めて擬似距離を平均し時計推定に使用している様である。
擬似距離マルチパスの相対値は搬送波位相を基準にして容易に推定できるので、全マルチパスの平均=0の様な一定の制約を仮定するとマルチパスの絶対値を推定することが出来る。GTにおいてもこの手法で推定した擬似距離マルチパスを使って擬似距離を補正することも可能であるが、擬似距離マルチパス補正を行った時計推定値とIGS
Clockとの間には明らかなバイアス誤差が認められる。これはIGS
Clockがマルチパス補正を行っておらずマルチパスを含めた擬似距離平均を時計推定に使用しているためと考えられる。
厳密に言えば観測局によりマルチパスの大きさや出方は異なるのでマルチパスを含めた擬似距離平均を使って決定される時計推定値は使用した観測局セットによって差が出るはずである。しかし現在までの解析では陽にその様な差は見られていない。
さらに複雑なことにGPSでは原理上衛星時計と受信機時計の差しか計測できないので特定時計を基準とした相対時計しか決定することが出来ない。従って通常は特定の基準時計局の時計を0に固定して相対時計を推定する。基準時計局の選び方は任意であるがなるべく高安定時計を持った局を選定するのが普通で、IGSの解析でも水素メザー原子時計を装備した局を基準時計局とすることが多い。なおこの方法は時計基準局時計が故障したり観測データが欠落したりした場合、全体の時計推定が破綻したり誤差が増大するので、基準時計局の状態を監視し異常の場合別の基準時計局に切り替えたり、最初から複数の基準時計の重み付き平均を基準として時計を推定する場合もある。
このようにGPS衛星及び受信機ネットワーク内で決定された相対時計は最終的にUTCやGPS時刻への対応づけがなされる。IGS
Clockの場合は各解析センタで推定された相対時計を調整併合するのと同時に複雑な手順で最終的にGPS時刻系に合わせる。この手順の詳細についてはJ.Ray,K.Senior,
IGS/BIPM pilot project: GPS carrier phase
for time/frequency transfer and timescale
formation, Metrologia 40 (2003) S270-S288に詳しい。厳密に言えばGPS時刻は放送暦以上の精度を持たないのでIGS
Clockの時刻系はIGRT(Rapid Clock)またはIGST(Final
Clock)と呼ばれる。時計が推定期間中の擬似距離平均値を基に決定されること及びGPS時刻との対応付けが解析期間毎に行われることよりIGS
Clockには24H毎00:00GPSTにおいて時刻の不連続が見られる。場合によっては時刻不連続が問題になること時刻系を直接UTCに対応付ける方が何かと都合が良いことからIGSでも時刻決定プロセスの改善検討がされており、将来的にはこれらのプロセスが変更になる可能性が高い。
さて、この絶対時刻との対応付けは測位の面では必ずしも必要とはならない。PPPの場合でも衛星時計の相対差が精密に決定されていればよく、受信機時計推定値を使わない場合あるいは使う場合でも受信局間の相対差しか必要でない場合、必ずしも絶対時刻は必要とされない。従って通常相対時刻として決定されている解析センタ解もPPPで使用することが出来る。なおこの際、受信機時計は使用した衛星時計の時刻系に従って推定されることになる。
GPS観測データを使った時計決定手順については多分解析ソフトウェアによって異なるが詳細が公開されているものはほとんどない。以下にGTで使用している時計推定手順をまとめる。なおこの手順はGTの開発に当たって試行錯誤しながら導出したもので最終的に推定値はIGS
Clockに0.15nsの精度で一致している。
・C1擬似距離観測値にP1-C1バイアス補正を行いP1相当擬似距離を生成する。
・搬送波位相観測値のcycle-slip検出を行う。cycle-slipを検出した場合前後を別アークとして識別する。
・P1-P2電離層フリー擬似距離をL1-L2電離層フリー搬送波位相を使ってスムージングする。
・スムージングしたP1-P2電離層フリー擬似距離を使ってパラメータ推定を行う。
・衛星時計は1st order Gauss-Marcov、受信機時計はrandom-walk過程でモデル化し推定する。衛星時計初期値は放送暦、受信機時計初期値はコードと放送暦を使った単独測位で求める。
・同時にアーク毎搬送波位相バイアス残差を固定値として推定する。ここで初期値は0、初期標準偏差は1mとしている。
・推定終了後、衛星毎、観測局毎に搬送波位相バイアス残差推定平均値を時計推定値からバイアスとして差し引く。
スムージング擬似距離は相対値としては搬送波位相の精度を維持しているがアーク内のマルチパス平均値がバイアスとして乗っているためそれを固定搬送波位相残差として推定し落としている。推定時計そのままでは時計にバイアスが残るため、最後に搬送波位相と擬似距離の差分をバイアス残差推定値の平均を使って補正している。
.....................................................................................................................................
擬似距離バイアス
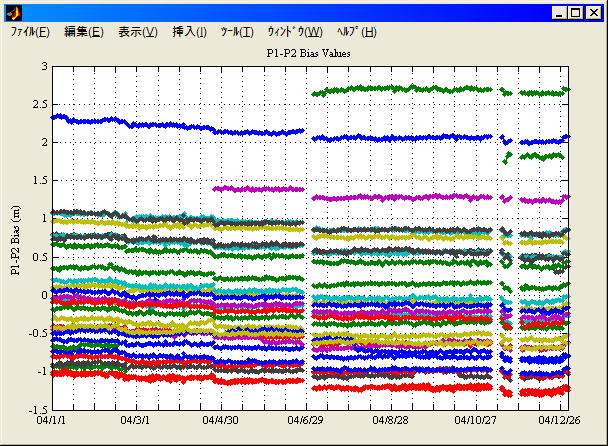
P1-P2バイアス
P1-P2バイアスIGS推定値1年分。IGS TEC Finalから抜き出している。衛星DCBの和が0になるように正規化しているので衛星が切り替わったタイミングで不連続が見られる。抜けているところは何故かIGS
TEC Finalがないところ。長期安定度もかなり良いが本当だろうか。

IGS P1-P2バイアス値(衛星) (2004/1/1-2004/12/31) (表示プログラム)
P1-C1バイアス
コードレス受信機にはいくつかの方式があり、方式により擬似距離測定値に差が見られる。IGSネットワークがRogue/TurboRogue(TR)を中心にした受信機から新世代のコードレス受信機に移行にあたり、擬似距離観測値にTRとのバイアスが見られるようになった。
詳細は以下のIGS Mailを参照のこと。
J.Kouba et al., Handling mixed receiver types, IGS Mail-2320, 24 Jun 1999
J.Ray, new pseudorange bias convention, IGS Mail-2744, 15 Mar 2000
P1-P2でIGS Clockが算出されるようになったのはGPS
Week 1056 (2000/04/02)からで、それまでのIGS
ClockはC1-P2で算出さていた。従ってGPS Week
1055以前のIGS Clockを使用するには注意が必要である。P1-C1バイアスの値については何度か更新されておりIGS
Clockを使う際にはIGS解析で使われたP1-C1バイアスを使って補正する必要がある。IGSでの解析で使用されているP1-C1バイアスの履歴とその値を以下に示す。
| 適用開始週 | cc2noncc.fバージョン | 参照IGS Mail | 備考 |
|---|---|---|---|
| GPS Week 1056 (2000/04/02) | ver.1.3 | IGS Mail-2744 | |
| GPS Week 1067 (2000/06/18) | ver.1.4 | IGS Mail-2879 | |
| GPS Week 1097 (2001/01/14) | ver.2.0 | IGS Mail-3160 | |
| GPS Week 1106 (2001/03/18) | ver.2.1 | IGS Mail-3220 | |
| GPS Week 1150 (2002/01/20) | ver.2.4 | IGS Mail-3674 | |
| ver.3.0 | IGS Mail-3737 | ||
| ver.3.2 | IGS Mail-4214 | ||
| GPS Week 1208 (2003/03/02) | ver.4.0 | IGS Mail-4279 | |
| GPS Week 1219 (2003/05/18) | ver.4.3 | IGS Mail-4366 | |
| GPS Week 1257 (2004/02/04) | ver.4.5 | IGS Mail-4825 | |
| GPS Week 1271 (2004/05/10) | ver.4.6 | IGS Mail-4937 | |
| GPS Week 1284 (2004/08/15) | ver.4.7 | IGS Mail-4987 | |
| GPS Week 1306 (2005/01/16) | ver.4.8 | IGS Mail-5078 |
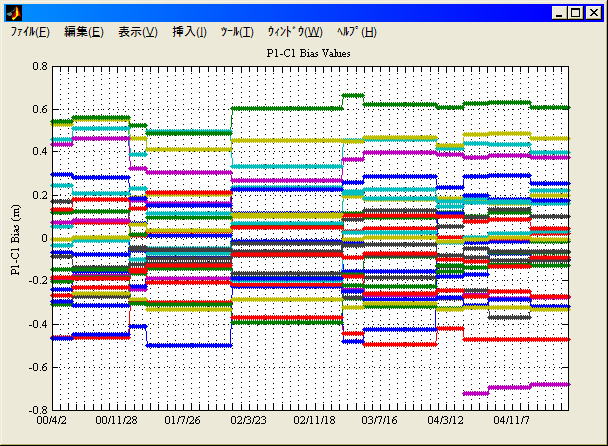
IGS P1-C1バイアス値 (2000/4/2-2005/6/1) (表示プログラム)
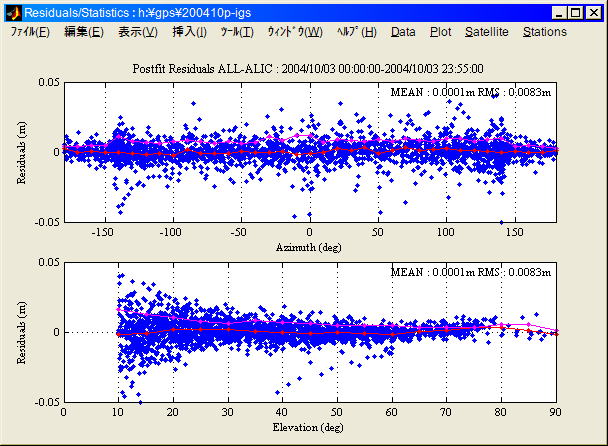
推定残差-方位仰角依存性(例) (2004/10/3 24H
PPP, 観測局:ALIC) (赤: 平均、ピンク: 標準偏差)
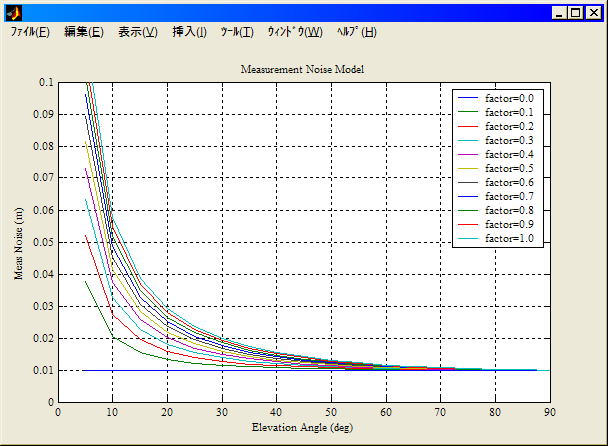
観測ノイズモデル (表示プログラム)
| 解析ID | factor | 軌道推定誤差 | 備考 |
|---|---|---|---|
| 200410c-test6 | 1.0 | 5.52cm | |
| 200410c-test7 | 0.6 | 5.52cm | |
| 200410c-test8 | 0.3 | 5.53cm | |
| 200410c-test9 | 0.1 | 5.58cm | |
| 200410c-test10 | 1.5 | 5.61cm |
.....................................................................................................................................
測位モードによる時間感度の差
・2004/10/23 00:00〜23:55, 電子基準点950242 新潟大和
・GT0.5.5alpha 5分間隔24H、IGS Final Orbi/Clock使用、clock
jumpリペア有、backwardフィルタ有
・新潟県中越地震発生時刻: 2004/10/23 8:57UTC
Kinematic PPPモード
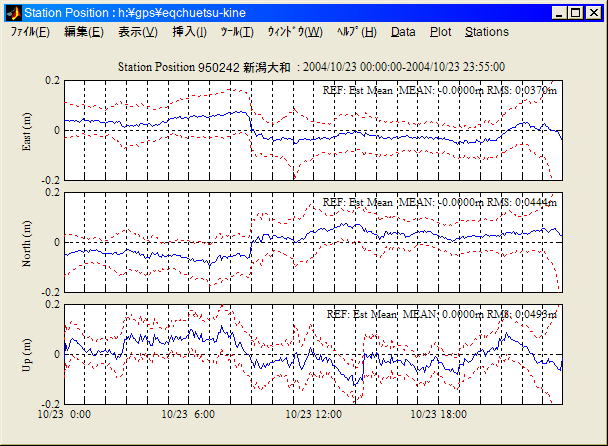
Static PPPモード (局位置プロセスノイズ=1mm/sqrt(sec))
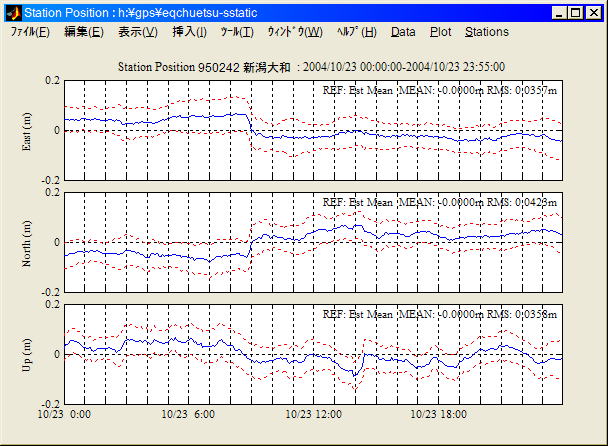
Static PPPモード (局位置プロセスノイズ=0.3mm/sqrt(sec))
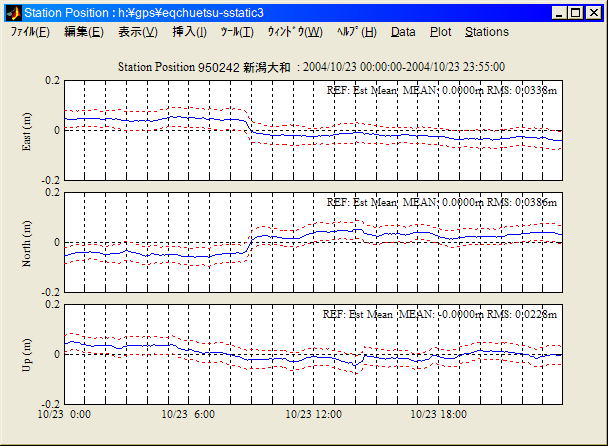
Static PPPモード (局位置プロセスノイズ=0.1mm/sqrt(sec))
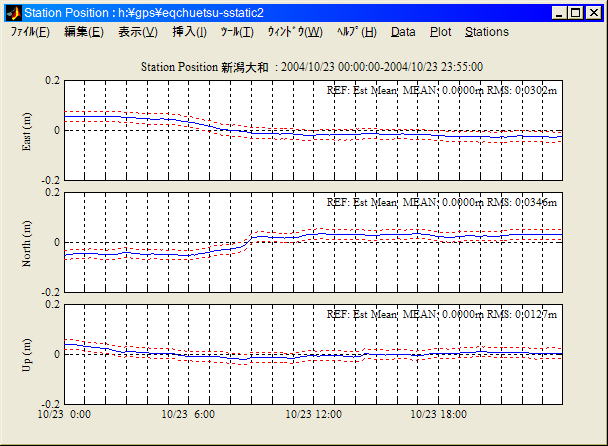
Static PPPモード (局位置プロセスノイズ=0mm/sqrt(sec))
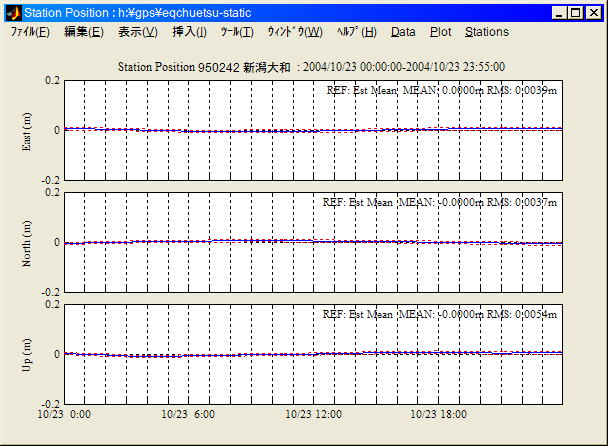
(本解析には国土地理院電子基準点データを使用しました)
.....................................................................................................................................
Static PPPにおける局位置プロセスノイズパラメータ
局位置はrandom-walk過程でモデル化しているので1Hで10cm(1σ)の変動がある場合の局位置プロセスノイズは、
sqrt(0.1m^2/3600s)=0.0017m/sqrt(sec)
逆に1mm/sqrt(sec)のプロセスノイズの場合、1H後の位置の不確定性(1σ)は
sqrt(0.001m/sqrt(sec)^2*3600s)=0.06m
上記中越地震による新潟大和の位置変動についてstatic
PPP, プロセスノイズ=1mm/sqrt(sec)の場合、水平10cm程度の変動があり収束に1〜1.5Hかかっているから大体一致する。
kinematic PPPの場合もっと変動がシャープに出るはずだが実際にはかなりなまっている。これは対流圏遅延を推定している影響かもしれない。
.....................................................................................................................................
Clock Steeringに伴う擬似距離観測値の飛び
水晶発振器をクロック基準として使用したGPS受信機には受信機クロックのドリフトが大きいものがある。GPS観測データのサンプリングタイミングは受信機クロックに基づいて決められるが、これらの受信機では何も対策しないとこのタイミングがGPS時刻からどんどんずれていってしまうという問題が有る。これらの受信機の中には、この問題に対応するため一定以上クロック誤差が大きくなった場合に自動的に受信機クロックを操作しGPS時刻に合わせこむという動作をするものがある。この動作はClock
Steeringと呼ばれる。
これらの動作の詳細は多分に受信機に依存するが、一般的には受信機クロックとGPS時刻との差が0.5msを超えたタイミングで正確に1ms受信機クロックをずらす動作をするものが多い。現在確認した中でこれらの動作を行う受信機は以下の通り:AZTECH UZ-12, TRIMBLE4000SSI, TRIMBLE4700, TRIMBLE5700。なお、受信機によってはこの機能をOFFに設定でき、原子時計等の外部クロックを接続する場合は通常OFFに設定されるため、これらの受信機でもClock Steeringが発生しない場合も有る。
Clock Steeringは受信機クロックの飛びであるから、観測データに影響が現れる。この動作の観測データへの出方は2種類ある。
(1) Clock Steering時に擬似距離観測値に1msの飛びが現れる。Time
Tag Offset=0のまま。(例 NOUM, AZTECH UZ-12)
(2) Clock Steering時に擬似距離観測値に飛びは現れない。Time
Tag Offsetに1msの飛びが現れる。(例 GLSV, TRIMBLE4000SSI)
擬似距離観測値を生成する際の受信機クロック誤差をTime Tagで示された受信時刻を基準に測ると考えれば(1), (2)は等価である。
また現在確認している範囲では、Clock Steering時に搬送波位相観測値には飛びは発生しない。
さて(2)の場合、RINEX観測データ出力時のTime Tag Offsetの初期値は多くの場合0となるようだ。従って、例えば1時間毎に出力したのRINEX観測データを併合して、24時間分のRINEX観測データを作った場合、元の観測データファイル内ではClock Steering時の擬似距離観測値の飛びは発生しないが、複数の観測データファイルの切り替えタイミング、すなわちこの場合1時間毎に、Time Tag Offsetが0にリセットされると同時に擬似距離観測値に飛びが現れる (例 電子基準点, TRIMBLE5700)。これは、例えば24時間RNIEX観測データを3日間分結合して解析する様な場合にも同じ現象が発生する。
受信機クロックの飛びが搬送波位相観測値に反映されないことや受信機クロック誤差の一部をTime Tag Offsetに逃がすことがRINEXフォーマット上正しいのかどうかは仕様を読んだだけでは曖昧であるが、現実には許容されているようだ。またここで書いた事項が全てのSteered Clock受信機に当てはまるかどうかは不明である。もしかすると異なる動作をする受信機がある可能性もある。
さて、これらの受信機において擬似距離観測値に飛びが現れること及び搬送波位相観測値には飛びは発生しないことは観測データ処理上は幾つかの問題を引き起こす。
(1) 擬似距離観測値を使ってサイクルスリップ検出している場合、受信機クロック飛びをサイクルスリップと誤判定してしまう。
(2) 擬似距離観測値にのみ飛びが現れ搬送波位相観測値に飛びが現れないことから、両者を使った線形結合に飛びが現れる。これを観測量として推定を行う場合に大きな誤差要因となる。
これらの問題に対応するため、一般に使われている観測データ前処理プログラムはClockPrepである (参考:IGSMAIL-4318)。このプログラムの動作の詳細はよく分からないがHelp等を読む限り、擬似距離観測値の飛びを検出して飛びを直すと同時に、それと矛盾しないようにTime Tagを修正しているだけの様である。この処理により、擬似距離観測値に飛びが消え、搬送波位相観測値との矛盾も解消される。期間の長い観測データではTime Tag Offsetがどんどん累積されて大きくなっていくが、搬送波位相観測値を使った精密解析では観測データの受信時刻の決定には擬似距離観測値による単独測位が使われ、Time Tagは受信時刻の概算決定にしか使われないので通常問題とならない。
GTにおいても幾つかの方式を評価したが、最終的にはClockPrepと似たような以下の方法で補正している。
(1) 観測エポック毎に擬似距離による単独測位で受信機クロック誤差を求める。ここで求められる値はGPS時刻に対する誤差である。
(2) 受信機クロック誤差のエポック間差の絶対値が0.5ms以上をクロック飛びと判定する。クロック飛び幅はクロック誤差エポック間差を1msの倍数に丸めて求める。
(3) クロック飛び以降のエポックの時刻タグからクロック飛び幅分を減算する。
(4) クロック飛び以降のエポックの擬似距離観測値からクロック飛び幅分を減算する。
(5) クロック飛び以降の受信機クロック誤差推定値からクロック飛び分を減算する。
GTによる受信機クロック飛び補正の例を以下に示す。
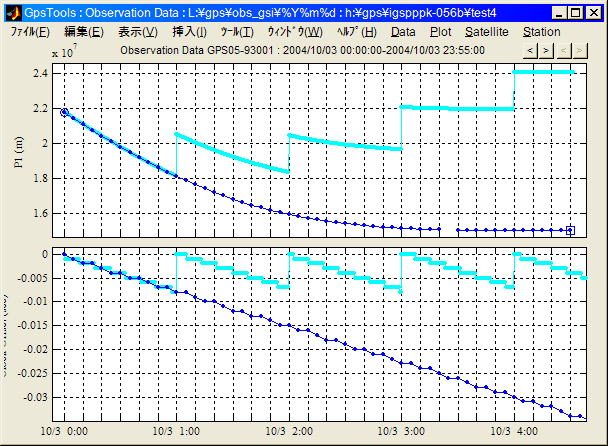
受信機クロック飛び補正例 (電子基準点:93001佐野,
受信機:TRIMBLE5700, 2004/10/3 0:00-4:40)
上段:P1擬似距離観測値, 下段:Time Tag Offset,
水色:補正前観測データ, 青:補正後観測データ
約8〜9分間隔でClock Steeringが発生し補正前データでは1時間毎にTime
Tag Offsetが0にリセットされて擬似距離観測値が飛んでいる。
.....................................................................................................................................
サイクルスリップ編集 (1)
Kinematic PPPにおいては搬送波位相観測値のサイクルスリップ検出が大変重要である。これはStatic
PPPの場合他のエポックの観測を使って測位解に強い拘束がかけられるのに比較し、Kinematicでは測位解が他エポックの測位解と独立となるため拘束を強くかけられないためである。Kinematic
PPPの場合、サイクルスリップ検出漏れはパルス上の大きな測位誤差となって現れる。サイクルスリップ検出漏れによる測位誤差の例を以下に示す。
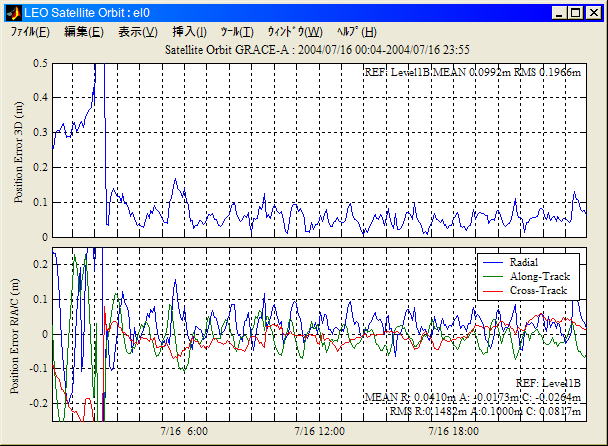
サイクルスリップ検出漏れによる測位誤差の例
GRACE-A Kinematic PPP結果 2004/7/16 0:00〜2:30にかけて大きな測位誤差が見られる
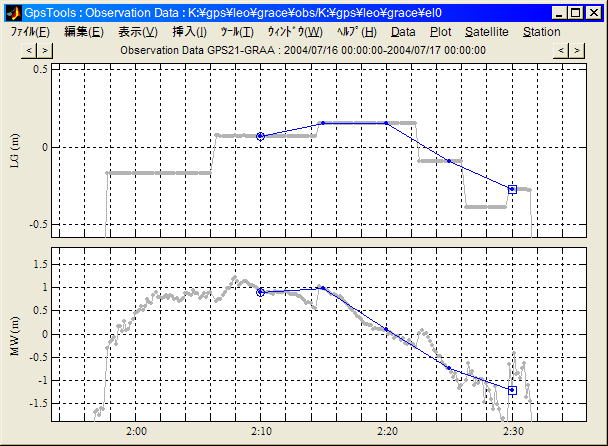
同上PRN21衛星 搬送波位相観測値のLG(幾何学フリー線形結合)及びMW(Melbourne-Wubbena線形結合)
2:14, 2:22, 2:26, 2:29のタイミングで明らかなサイクルスリップが見られるが検出できていない
(灰色: 生観測データ(10秒間隔), 青: 編集済観測データ(300秒間隔),
○:アーク開始, □:アーク終了)
サイクルスリップ検出漏れは以上のように大きな測位誤差となって現れるが、サイクルスリップの誤検出(過検出)も測位精度の悪化となって現れる。これはサイクルスリップ補修を行わない場合はアーク長が短くなり、アーク内の独立性の高い観測データ数が減り、推定条件が悪くなることによる。例えば同時5衛星が観測できる場合、アークは最低でも3エポック以上の観測データを持つ必要があり。(観測データ数5×3=15,
推定パラメータ数: 測位解3×3+搬送波位相バイアス5=14)。また一般に時刻の近いエポックの観測データには相関の高い誤差が含まれることが多いため、サイクルスリップによるアーク分断及び短アーク化はこの点でも推定条件を悪化させる。サイクルスリップ補修を行う場合、条件にもよるが誤補修を完全になくすことが難しく、誤補修はサイクルスリップ検出漏れと同様の精度悪化を引き起こす。
以上より、特にKinematicの場合、サイクルスリップ検出アルゴリズムは検出漏れは無くし、誤検出も最小にするという背反する要求を満足する必要がある。
さて相対測位の場合、サイクルスリップ検出は推定時と同様に搬送波位相観測値の二重差を作ってから検出を行うことが多い。これは衛星時計、受信機時計変動や各種の誤差要因が消去されるためサイクルスリップ検出が容易になるためである。
PPPの場合、二重差が使えないのでゼロ差搬送波位相観測値のままサイクルスリップ検出を行う必要がある。サイクルスリップ検出には幾つかの方式が考えられるが一般には複数の方式を組み合わせて用いられる。これは検出精度を上げるためと、単独ではL1,L2搬送波位相のどちらが飛んだか判定できず、L1,L2搬送波位相それぞれのスリップ量の推定も出来ないことによる。
サイクルスリップ検出に使われる主な方式を以下に示す。
(1) LG(搬送波位相幾何学フリー線形結合)飛び検出
(2) MW(Melbourne Wubbena Wide Lane線形結合)飛び検出
(3) LC(搬送波位相電離層フリー線形結合)-PC(擬似距離電離層フリー線形結合)の飛び検出
(4) WL(Wide Lane線形結合)エポック間3重差
(5) NL(Narrow Lane線形結合)エポック間3重差
LGは幾何学項(軌道, 衛星/受信機時計, 対流圏遅延)が消去され、かつ搬送波しか使用していないため擬似距離マルチパスの影響を受けない。従ってサイクルスリップによる飛びを判定しやすい。ただし電離層遅延項が残っているため電離層遅延の変動が激しい場合や観測エポック間隔が大きい場合にはサイクルスリップと電離層遅延変動の切り分けが難しい。
MWは幾何学項及び電離層遅延項が消去されているが擬似距離マルチパスの影響が大きく擬似距離観測条件に強く依存する。
LC-PCはMWに比べても雑音が大きい。
WL/NLエポック間3重差は受信機の時計が原子時計でない場合、受信機時計変動とサイクルスリップの切り分けが難しい。またLEO衛星の様な高速移動体の場合も同様の理由でサイクルスリップの切り分けが難しい。
(この項続く)
.....................................................................................................................................
サイクルスリップ編集 (2)
サイクルスリップ検出困難な事例。この衛星を除外するとKinematic
PPP測位解の大きな誤差がなくなるので6:55にスリップしていることは間違いないがLG飛び1cm以下。MWもマルチパスで鈍っていて1cycle
(86cm) 飛んでいるか微妙。
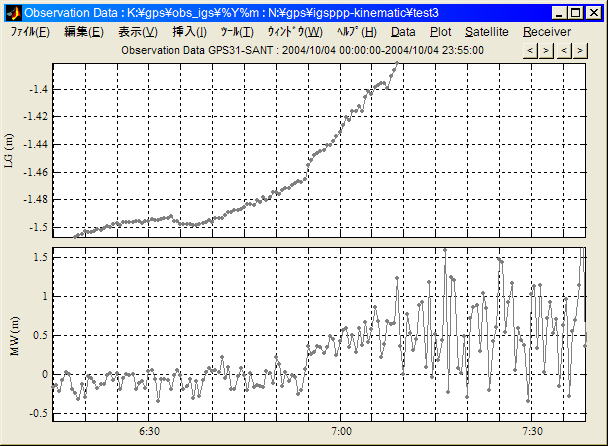
サイクルスリップ検出困難な事例 (2004/10/4
SANT PRN31観測データ)
上段: 幾何学フリー線形結合、下段: Melbourne
Wubbena線形結合、6:55にサイクルスリップが発生している。
L1/L2サイクルスリップとLG飛び量の関係。(1,1),
(4,3), (5,4), (8,6), (9,7), (10,8), (13,10),
(14,11) はLGでは検出が難しいが、MW WLでは(4,3),
(4,5) は1cycle (86cm), (8,6), (9,7), (10,8),
(13,10), (14,11)は2cycle (172cm) 以上飛ぶので(1,1)以外は通常は検出できるはず。上の事例は(4,3)
かまたは(-1,-1)か? でもLG飛びが小さすぎる。
| L1/L2 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | -24.4 | -48.8 | -73.3 | -97.7 | -122.1 | -146.5 | -170.9 | -195.4 | -219.8 | -244.2 | -268.6 | -293.1 | -317.5 | -341.9 | -366.3 |
| 1 | 19.0 | -5.4 | -29.8 | -54.2 | -78.7 | -103.1 | -127.5 | -151.9 | -176.3 | -200.8 | -225.2 | -249.6 | -274.0 | -298.4 | -322.9 | -347.3 |
| 2 | 38.1 | 13.6 | -10.8 | -35.2 | -59.6 | -84.0 | -108.5 | -132.9 | -157.3 | -181.7 | -206.2 | -230.6 | -255.0 | -279.4 | -303.8 | -328.3 |
| 3 | 57.1 | 32.7 | 8.2 | -16.2 | -40.6 | -65.0 | -89.4 | -113.9 | -138.3 | -162.7 | -187.1 | -211.5 | -236.0 | -260.4 | -284.8 | -309.2 |
| 4 | 76.1 | 51.7 | 27.3 | 2.9 | -21.6 | -46.0 | -70.4 | -94.8 | -119.3 | -143.7 | -168.1 | -192.5 | -216.9 | -241.4 | -265.8 | -290.2 |
| 5 | 95.1 | 70.7 | 46.3 | 21.9 | -2.5 | -27.0 | -51.4 | -75.8 | -100.2 | -124.6 | -149.1 | -173.5 | -197.9 | -222.3 | -246.7 | -271.2 |
| 6 | 114.2 | 89.8 | 65.3 | 40.9 | 16.5 | -7.9 | -32.3 | -56.8 | -81.2 | -105.6 | -130.0 | -154.5 | -178.9 | -203.3 | -227.7 | -252.1 |
| 7 | 133.2 | 108.8 | 84.4 | 59.9 | 35.5 | 11.1 | -13.3 | -37.7 | -62.2 | -86.6 | -111.0 | -135.4 | -159.8 | -184.3 | -208.7 | -233.1 |
| 8 | 152.2 | 127.8 | 103.4 | 79.0 | 54.6 | 30.1 | 5.7 | -18.7 | -43.1 | -67.6 | -92.0 | -116.4 | -140.8 | -165.2 | -189.7 | -214.1 |
| 9 | 171.3 | 146.8 | 122.4 | 98.0 | 73.6 | 49.2 | 24.7 | 0.3 | -24.1 | -48.5 | -72.9 | -97.4 | -121.8 | -146.2 | -170.6 | -195.1 |
| 10 | 190.3 | 165.9 | 141.5 | 117.0 | 92.6 | 68.2 | 43.8 | 19.3 | -5.1 | -29.5 | -53.9 | -78.3 | -102.8 | -127.2 | -151.6 | -176.0 |
| 11 | 209.3 | 184.9 | 160.5 | 136.1 | 111.6 | 87.2 | 62.8 | 38.4 | 14.0 | -10.5 | -34.9 | -59.3 | -83.7 | -108.2 | -132.6 | -157.0 |
| 12 | 228.4 | 203.9 | 179.5 | 155.1 | 130.7 | 106.2 | 81.8 | 57.4 | 33.0 | 8.6 | -15.9 | -40.3 | -64.7 | -89.1 | -113.5 | -138.0 |
| 13 | 247.4 | 223.0 | 198.5 | 174.1 | 149.7 | 125.3 | 100.9 | 76.4 | 52.0 | 27.6 | 3.2 | -21.2 | -45.7 | -70.1 | -94.5 | -118.9 |
| 14 | 266.4 | 242.0 | 217.6 | 193.1 | 168.7 | 144.3 | 119.9 | 95.5 | 71.0 | 46.6 | 22.2 | -2.2 | -26.6 | -51.1 | -75.5 | -99.9 |
| 15 | 285.4 | 261.0 | 236.6 | 212.2 | 187.8 | 163.3 | 138.9 | 114.5 | 90.1 | 65.7 | 41.2 | 16.8 | -7.6 | -32.0 | -56.5 | -80.9 |
上の事例、それではTEQCでは検出できるのだろうかと思ってやってみた(TEQCオプション : teqc +qc +set_mask 0 +ssv +sym +l -plot)。 スリップ検出数48。やはり検出できない。TEQCは標準設定ではサイクルスリップ検出が甘すぎる。ちなみにGTの観測データ編集結果 (ログ)。スリップ検出数259。結局A/S onの状態では擬似距離マルチパスが大きくかなり条件のよい局でも完全なサイクルスリップ検出は困難だということ。この辺はある程度割り切る必要がある。
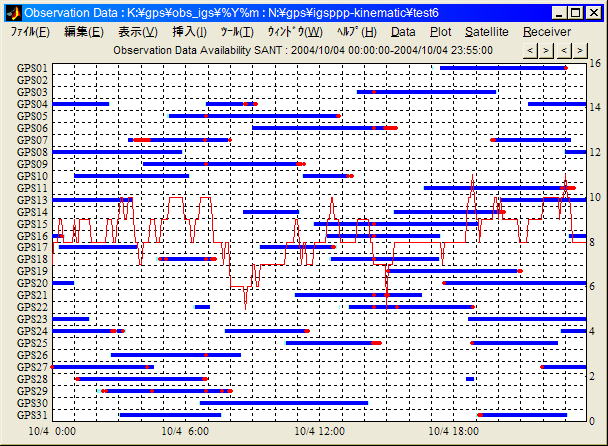
GTによるSANT 2004/10/4観測データ編集結果
青線 : 有効観測データ有, 赤点 : サイクルスリップ,
赤線 : 観測衛星数
.....................................................................................................................................
GPS精密解析でよく使われるL1,L2搬送波位相及び擬似距離観測値の線形結合を以下に示す。各線形結合の定義については別紙参照。表内のTypical Noise+Multipathは平均的な値であるが、擬似距離マルチパスは特に低仰角で大変大きくなることがあり、固定局でも最大で数mに達することがありその際はMW,
MP1, MP2のノイズ成分もそれに応じて大きくなるので注意が必要である。
| LC | Linear Combination | Wave Length | Relative Ionosphere | Typical Noise+Multipath |
|---|---|---|---|---|
| L1 | L1 Carrier Phase | 19.0cm | 1.0 | 0.3cm |
| L2 | L2 Carrier Phase | 24.4cm | 1.6 | 0.3cm |
| LG | Geometry-free Phase | - | 0.6 | 0.4cm |
| LC | Ionosphere-free Phase | - | 0.0 | 0.9cm |
| MW | Melbourne-Wubbena | 86.2cm | 0.0 | 21cm |
| WL | Wide-lane Phase | 86.2cm | 1.3 | 1.7cm |
| NL | Narrow-lane Phase | 10.7cm | 1.3 | 1.7cm |
| MP1 | L1 Multipath | - | 0.0 | 30cm |
| MP2 | L2 Multipath | - | 0.0 | 30cm |
(Assumption : Typical Noise+Multipath : L1=0.3cm, L2=0.3cm, P1=30cm, P2=30cm)
サイクルスリップ編集(2)で書いた検出困難なスリップの例はMP1またはMP2線形結合を使うとうまく検出できることが分かった。MP1,MP2線形結合の飛びを以下に示す。なおTEQCは取説を読む限りLG+MP1+MP2飛びでサイクルスリップを検出している様だ。
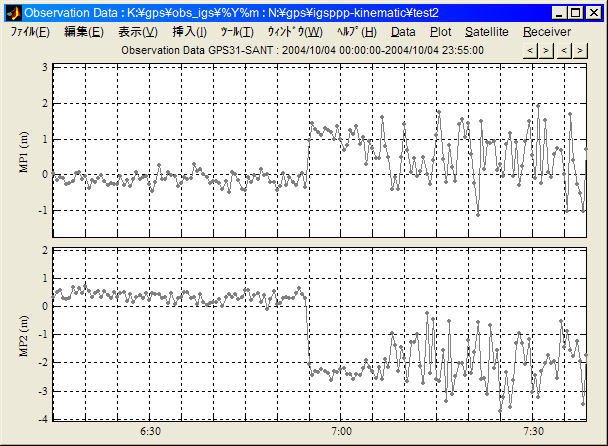
サイクルスリップ検出例 (2004/10/4 SANT PRN31観測データ)
上段: L1 Multipath線形結合、下段: L2 Multipath線形結合、6:55にサイクルスリップが発生している。
L1,L2サイクルスリップによるLG, MW, MP1, MP2の飛び量を別紙に示す。(出力プログラム)
.....................................................................................................................................
現在インターネットを介して利用できる主なオンラインGPS精密解析サービス及びその特徴を以下に示す。解析を依頼するにはRINEX観測データをWebからまたはFTPにより解析サーバにuploadする。解析結果はEmailまたはFTPで取得することが出来る。観測データ形式としてCompact RINEX及びgzip,compress等の圧縮ファイルもサポートしている。OPUS以外は全世界の観測点の精密測位が可能である。
| Service | Provider | Analysis Eng. | Strategy | Ref. Frame | Ref. Stas | Note |
|---|---|---|---|---|---|---|
| AUSPOS | Geosience Australia (豪) | MicroCosm(R) | 相対測位 (Static) |
ITRF | 近隣IGS局3局 | 24H精度水平1cm,垂直1-2cm |
| SCOUT | SOPAC (米) | GAMIT | 相対測位 (Static) |
ITRF,WGS84 | 近隣3局 | |
| OPUS | NGS (米) | page5 | 相対測位 (Static) |
ITRF, NAD83 | 近隣CORS3局 | サポートは米国及び一部領域内のみ |
| AUTO GIPSY | NASA JPL (米) | GIPSY/OASIS-II | PPP (Static) |
ITRF, WGS84 | - | uploadはanonymos FTPアドレス指定 |
| CSRS-PPP | CSRS (加) | CSRS-PPP | PPP (Static/Kinematic) |
ITRF, NAD83 | - | 要ユーザ登録 時計/対流圏同時推定 |
オンラインGPS精密解析サービスの精度を評価するため、同一のGPS観測データをオンラインGPS精密解析サービスを使って解析し、その結果を比較した。データとしては2004/10/3
24H 30秒間隔の国土地理院 電子基準点960698 玉之浦の観測データを使用した。解析条件としては24H
Static測位とし、アンテナ機種が指定可能なものはAOAD/M_Tとした。解析結果及びGT
PPP解を基準とした誤差も示す。参考のため国土地理院F2解の値も同時に示した。表中でAUTO
GIPSYの測位解はアンテナ位相中心のものでありアンテナオフセットを補正していない。従って他と同一基準で評価するためにはオフセット分垂直座標82mmを差し引く必要がある。
| Service/ Solution |
ITRF2000 Position | Error wrt GT PPP | Note | ||||
|---|---|---|---|---|---|---|---|
| X (m) | Y (m) | Z (m) | E (mm) | N (mm) | U (mm) | ||
| GT PPP | -3355701.7822 | 4200702.9589 | 3419893.7309 | 0.0 | 0.0 | 0.0 | |
| AUSPOS | -3355701.783 | 4200702.963 | 3419893.740 | -1.9 | +5.7 | +8.0 | ref:DAEJ,SUWN,SHAO |
| SCOUT | -3355701.7828 | 4200702.9676 | 3419893.7398 | -5.0 | +3.6 | +10.8 | ref:DAEJ,SUWN,SHAO |
| OPUS | -3355701.784 | 4200702.955 | 3419893.746 | +3.8 | +13.8 | +6.5 | out of service range |
| AUTO GIPSY | -3355701.8305 | 4200703.0400 | 3419893.7863 | -12.9 | -3.8 | +108.6 | without antenna offset |
| CSRS-PPP | -3355701.7910 | 4200702.9647 | 3419893.7317 | +3.3 | -4.7 | +8.9 | |
| GSI F2解 | -3355701.8161 | 4200702.9610 | 3419893.7359 | +25.2 | -8.1 | +21.9 | |
.....................................................................................................................................
擬似距離観測モデル
P=ρ+c(dt-dT)+I+T+ε
において受信機時計誤差dt,衛星時計誤差dTは何を表しているかを考えてみる。
受信機では受信機時計に従って一定時間間隔で受信測位コード位置を測定する。より厳密には受信したPRNコードに同期させたレプリカPRNコードのコードシーケンス上の位置を測定する。ただしその測定タイミングの絶対時刻tr'と受信機時計での測定時刻tr(これは普通端数はでない)との差が時計誤差と言うわけではない。ρはアンテナ位相中心間距離として定義されるから観測モデルを上記のように書くためには、時間を遡ってみて測定した測位コード(の位置)が搬送波に載って受信アンテナ位相中心に入射したタイミングの絶対時刻tと受信機時計での測定時刻trの差を受信機時計誤差dtとしなければならない。従ってdtには本来の受信機時計誤差に加え受信ケーブル遅延や受信機回路遅延Δtrが含まれる。これらの遅延は一般にコードにより異なるから、時計は一つだとしてもコードが異なると時計誤差dtも異なることになる。擬似距離バイアス(受信機DCB)は主にこの遅延の差により生じる。(なお受信コードとレプリカコードの同期誤差もあるはずだがこれは観測誤差として扱うのが妥当である)
それでは衛星時計誤差dTとは何か。測定した測位コード位置が表す時刻tsとこの測位コードの載った搬送波が衛星アンテナの位相中心を出発した絶対時刻(t-τ)との差としなければならない。これも測位コード位置が表す時刻tsと衛星での測位コード生成タイミングの絶対時刻ts'の差ではない。受信機と同様に回路遅延や送信ケーブル遅延Δtsが含まれる。これが衛星DCBが生じる原因となる。
なお以上はあくまで観測モデルを上の様に書くための定義であり直感的な時計の意味とは異なっている。数式で表してみよう。
dt1=tr-t1=tr-tr'+Δtr1
dt2=tr-t2=tr-tr'+Δtr2
dT1=ts1-(t1-τ)=ts1-(ts1'+Δts1)
dT2=ts2-(t2-τ)=ts2-(ts2'+Δts2)
DCBr=Δtr1-Δtr2=dt1-dt2
DCBs=Δts2-Δts1≒dT1-dT2 (ts1-ts1'≒ts2-ts2')
P1-P2電離層フリー線形結合で時計誤差dt,dTを定義するとして
dt=C1*dt1+C2*dt2=dt1-C2*DCBr=dt2+C1*DCBr
dT=C1*dT1+C2*dT2=dT1-C2*DCBs=dT2+C1*DCBs
(C1=f1^2/(f1^2-f2^2),C2=-f2^2/(f1^2-f2^2))
P1=ρ+c(dt1-dT1)+I1+T+ε1=ρ+c(dt-dT)+I1+T+ε1-c*C2*(DCBr-DCBs)
P2=ρ+c(dt2-dT2)+I2+T+ε2=ρ+c(dt-dT)+I2+T+ε2+c*C1*(DCBr-DCBs)
PC=C1*P1+C2*P2=ρ+c(dt-dT)+T+ε (ion-free擬似距離)
厳密に言えばケーブル・回路遅延も時間変動するだろうから時計誤差にはそれらの変動も含まれていると言える。
ここで重要なのは
・時計はアンテナ位相中心で定義する。
・時計誤差にはケーブル・回路遅延が含まれている
・どのコードで時計誤差を定義したかによりその値が変わる。
ことである。
時刻同期にGPSを使う場合、以上の様に時計誤差がアンテナ位相中心で求まるので、実際の時計誤差を求めるためにはケーブル・回路遅延分を補正してあげる必要がある。この値はGPS観測では求めようがないので別途計測して落とす。これらの遅延が変動しないよう精密時刻同期用には温度補償された特別のケーブルや受信機を使う様である。
(この項続く)
.....................................................................................................................................