|
搬送波位相測定値による精密測位の理論及び解析処理 |
Home |
A.4.2 精密測位のモデル
A.4.2.1 擬似距離及び搬送波位相
A.4.2.2 幾何学距離
A.4.2.3 衛星軌道及び衛星時計
A.4.2.4 電離層遅延
A.4.2.5 対流圏遅延
A.4.2.6 受信アンテナ位相中心
A.4.2.7 衛星アンテナ位相中心
A.4.2.8 局位置変動
A.4.2.9 Phase Wind-up効果
A.4.2.10 相対論効果
A.4.2.11 マルチパス及び観測誤差
A.4.2.12 線形結合
精密測位ではmmレベルの精度を達成するため使用するモデルに厳密な取り扱いが必要になる。以下に精密測位に使用されるモデルにつき説明する。
一般的なGPS/GNSS受信機において得られる測位信号の測定値は擬似距離(pseudorange)と呼ばれる。擬似距離はGPS/GNSS衛星から送信された測位信号中のPRN(Pseudo-Random
Noise)コードと呼ぶ測位コードにより測定された衛星と受信機間の測位信号伝搬時間に光速を掛けたものと定義される。擬似距離を![]() (m)としてその観測モデルは以下のように表すことができる。
(m)としてその観測モデルは以下のように表すことができる。
ここで![]() は真空中での光速(m/sec)、
は真空中での光速(m/sec)、![]() はそれぞれ受信機時計、衛星時計で測った測位信号の観測時刻及び送信時刻である。また
はそれぞれ受信機時計、衛星時計で測った測位信号の観測時刻及び送信時刻である。また![]() は衛星と観測点間の幾何学距離(m)、
は衛星と観測点間の幾何学距離(m)、![]() は受信機時計誤差(sec)、
は受信機時計誤差(sec)、![]() は衛星時計誤差(sec)、
は衛星時計誤差(sec)、![]() は電離層遅延(m)、
は電離層遅延(m)、![]() は対流圏遅延(m)、
は対流圏遅延(m)、![]() はマルチパスを含んだ擬似距離観測誤差(m)を表している。
はマルチパスを含んだ擬似距離観測誤差(m)を表している。
現在のGPS衛星からはL1、L2帯という二周波マイクロ波の搬送波を使って測位信号が送信されているが、一般的なGPS/GNSS受信機で利用可能な測位コードはL1帯を使って送信されるC/Aコードのみである。なお今後打ち上げられるGPS衛星では新しい搬送波や測位コードの追加が計画されている。
さて主に精密測量を目的とする精密測位用GPS/GNSS受信機は擬似距離に加えて搬送波位相
(carrier phase)と呼ばれる観測量を測定する機能を持つ。搬送波位相とは受信機で復調した測位信号の搬送波位相角を連続的に測定したものである。搬送波位相には擬似距離と同様に衛星と観測点間の距離情報が含まれているが、擬似距離に比較して高精度な測定が可能なため精密測位に使用される。搬送波位相を![]() (m)として、その観測モデルは以下のように表すことができる。
(m)として、その観測モデルは以下のように表すことができる。
搬送波位相![]() はcycleを単位にして測定されることが多いが、計算の取り扱いが楽なように搬送波波長
はcycleを単位にして測定されることが多いが、計算の取り扱いが楽なように搬送波波長![]() (m)を掛けて単位を距離のdimensionに変換している。なおここではA.4.2.6以降に示す精密補正項は省略している。
(m)を掛けて単位を距離のdimensionに変換している。なおここではA.4.2.6以降に示す精密補正項は省略している。
搬送波位相には擬似距離とは異なり搬送波位相バイアスと呼ぶ連続的な測定では固定値となるバイアスが含まれている。搬送波位相バイアス![]() (cycle)は受信機初期位相
(cycle)は受信機初期位相![]() (cycle)、衛星初期位相
(cycle)、衛星初期位相![]() (cycle)及び整数不定性(Integer Ambiguity)
(cycle)及び整数不定性(Integer Ambiguity)![]() を使って以下のように表すことができる。
を使って以下のように表すことができる。
搬送波位相バイアスは、後で示す相対測位において、搬送波位相の二重差をとることにより受信機および衛星初期位相の項が消去されて整数となるが、差をとらない場合には一般には整数にはならない。この点、誤って記述されている文献が多いので注意のこと。より厳密な、搬送波位相及び搬送波位相バイアスの定義とモデルの導出については/1/が詳しい。
測位信号が一時的に途切れたり、あるいは観測雑音が大きくなったりして、受信機において搬送波位相の測定が連続的に行えなくなった場合に、搬送波位相バイアスの整数不定性![]() に新しい値が導入され、搬送波位相測定値が飛ぶことがある。この現象をサイクルスリップ
(cycle slip) と呼ぶ。サイクルスリップの検出と修正は搬送波位相を使用した精密解析の重要な課題のひとつでありA.4.6.5で再び解説する。
に新しい値が導入され、搬送波位相測定値が飛ぶことがある。この現象をサイクルスリップ
(cycle slip) と呼ぶ。サイクルスリップの検出と修正は搬送波位相を使用した精密解析の重要な課題のひとつでありA.4.6.5で再び解説する。
精密測位用GPS/GNSS受信機にはL1、L2帯二周波測位信号の擬似距離及び搬送波位相を測定できるものがあり二周波受信機と呼ばれる。二周波の測位信号は後で述べる様に、電離層遅延の大きさが搬送波周波数に依存することを利用して、主に搬送波位相に含まれる電離層遅延の補正に使用される。
搬送波位相測定における観測誤差![]() は通常はcm以下の値であり、他の項を十分な精度で与えることによりcm以下の精度で衛星と観測点の間の距離を測定することができる。
は通常はcm以下の値であり、他の項を十分な精度で与えることによりcm以下の精度で衛星と観測点の間の距離を測定することができる。
幾何学距離![]() は衛星と観測点間の物理的な距離を表すものである。より厳密には幾何学距離は測位信号送信時の衛星アンテナ位相中心位置と測位信号受信時の受信アンテナ位相中心位置の間の慣性空間上での距離として定義される。以下単に衛星位置、観測点位置と言った場合は以上の意味を示すものとする。
は衛星と観測点間の物理的な距離を表すものである。より厳密には幾何学距離は測位信号送信時の衛星アンテナ位相中心位置と測位信号受信時の受信アンテナ位相中心位置の間の慣性空間上での距離として定義される。以下単に衛星位置、観測点位置と言った場合は以上の意味を示すものとする。
幾何学距離![]() (m)は以下に示す光差方程式 (Light-Time Equation)
と呼ぶ方程式を解くことにより求められる。
(m)は以下に示す光差方程式 (Light-Time Equation)
と呼ぶ方程式を解くことにより求められる。
![]() (A.4.4)
(A.4.4)
![]() ,
, ![]()
ここで![]() ,
,![]() は地球固定座標系での衛星及び観測点位置(m)を示す。また
は地球固定座標系での衛星及び観測点位置(m)を示す。また![]() は測位信号受信時刻であり、受信機時計で測った観測時刻
は測位信号受信時刻であり、受信機時計で測った観測時刻![]() から受信機時計誤差
から受信機時計誤差![]() (sec)を引いたものである。
(sec)を引いたものである。![]() は電波伝搬時間(sec)であり幾何学距離を光速で割ったものに等しい。
は電波伝搬時間(sec)であり幾何学距離を光速で割ったものに等しい。
幾何学距離と座標系との関係を図A.4.1に示す。この図において実線が測位信号受信時刻![]() の地球固定座標系、点線が測位信号送信時刻
の地球固定座標系、点線が測位信号送信時刻![]() の地球固定座標系である。
の地球固定座標系である。
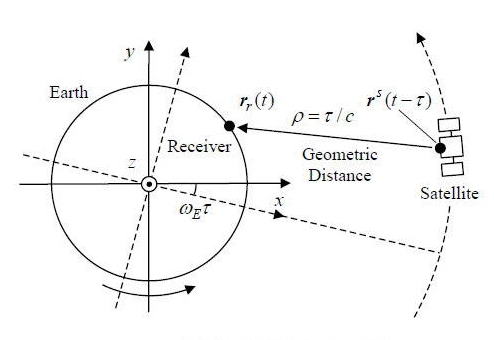
図 A.4.1 幾何学距離と座標系の関係
図に示すように、![]() を地球自転角速度
(rad/sec)として、地球自転により電波伝搬の間に地球固定座標系は慣性座標系に対し
を地球自転角速度
(rad/sec)として、地球自転により電波伝搬の間に地球固定座標系は慣性座標系に対し![]() (rad)回転する。(A.4.4)における測位信号送信時の衛星位置の計算にはその座標系回転分の補正
(rad)回転する。(A.4.4)における測位信号送信時の衛星位置の計算にはその座標系回転分の補正![]() が含まれている。ここで
が含まれている。ここで![]() は
は![]() を回転角としたz軸回りの座標系回転行列であり以下で定義される。
を回転角としたz軸回りの座標系回転行列であり以下で定義される。
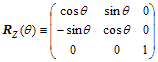
極運動により地球自転軸と地球固定座標の
z軸は、厳密には一致しないが、![]() は十分小さい値のためここではその差は無視している。
は十分小さい値のためここではその差は無視している。
さて、 (A.4.4)を解くことにより幾何学距離![]() を求めることができるが、この方程式は両辺に
を求めることができるが、この方程式は両辺に![]() を含むためそのままでは解くことができない、従って数値計算上は概略値を初期値にして逐次近似計算により解く。GPSの軌道では電波伝搬時間
を含むためそのままでは解くことができない、従って数値計算上は概略値を初期値にして逐次近似計算により解く。GPSの軌道では電波伝搬時間![]() の値は0.1 sec以下の値であり、
の値は0.1 sec以下の値であり、![]() を初期値にしても3〜4回の繰り返し計算で十分な精度で
を初期値にしても3〜4回の繰り返し計算で十分な精度で![]() を求めることができる。(A.4.4)を解くことにより電波伝搬時間
を求めることができる。(A.4.4)を解くことにより電波伝搬時間![]() が求められ同時に測位信号送信時刻及びその時刻における衛星位置も得られる。
が求められ同時に測位信号送信時刻及びその時刻における衛星位置も得られる。
ここで、 (A.4.4)式を解くためには受信機時計誤差![]() の値が必要になるが、精密測位ではこの値は別途、擬似距離測定値と放送暦を使った単独測位で求めることが多い。現在のS/Aオフの環境での単独測位による受信機時計誤差の推定精度は100
nsec程度であるが、GPS衛星の運動速度は4 km/sec程度、地球の自転による観測点の移動速度も赤道上で500m/sec程度であり、単独測位により求めた値でも(A.4.4)を解くには十分な精度を有している。ここで単独測位については本稿の範囲外であり適当な文献を参照のこと。なお、受信機時計誤差
の値が必要になるが、精密測位ではこの値は別途、擬似距離測定値と放送暦を使った単独測位で求めることが多い。現在のS/Aオフの環境での単独測位による受信機時計誤差の推定精度は100
nsec程度であるが、GPS衛星の運動速度は4 km/sec程度、地球の自転による観測点の移動速度も赤道上で500m/sec程度であり、単独測位により求めた値でも(A.4.4)を解くには十分な精度を有している。ここで単独測位については本稿の範囲外であり適当な文献を参照のこと。なお、受信機時計誤差![]() の大きさは多くの受信機で数msec以下に保たれており、衛星位置を放送暦で与える場合などで精度を要求されない場合にはこの項を無視することもある。
の大きさは多くの受信機で数msec以下に保たれており、衛星位置を放送暦で与える場合などで精度を要求されない場合にはこの項を無視することもある。
精密測位において衛星位置![]() は通常既知の値として衛星軌道情報から求める。観測点位置
は通常既知の値として衛星軌道情報から求める。観測点位置![]() は既知の値として与えられる場合と未知パラメータとして推定する場合がある。未知パラメータとして推定する場合、観測点が地球に対し静止しており観測点位置
は既知の値として与えられる場合と未知パラメータとして推定する場合がある。未知パラメータとして推定する場合、観測点が地球に対し静止しており観測点位置![]() が時刻に関わらず一定の値の場合をスタティック測位、観測点が移動体であり観測点位置
が時刻に関わらず一定の値の場合をスタティック測位、観測点が移動体であり観測点位置![]() が時刻によって変動する場合をキネマティック測位と呼ぶ。キネマティック測位で求められる観測点位置
が時刻によって変動する場合をキネマティック測位と呼ぶ。キネマティック測位で求められる観測点位置![]() は時計誤差を含んだ受信機時計に同期した時刻
は時計誤差を含んだ受信機時計に同期した時刻![]() での値が得られることに注意すべきである。高速移動体の位置を時計誤差を含まない時刻で求めたい場合、補間等により受信機時計誤差を補正するか適当な運動モデルを導入する必要がある。
での値が得られることに注意すべきである。高速移動体の位置を時計誤差を含まない時刻で求めたい場合、補間等により受信機時計誤差を補正するか適当な運動モデルを導入する必要がある。
さて、観測点位置![]() を未知パラメータとして推定する場合に、幾何学距離
を未知パラメータとして推定する場合に、幾何学距離![]() を観測点位置
を観測点位置![]() で偏微分した係数
で偏微分した係数![]() が必要になるので以下に示しておく。
が必要になるので以下に示しておく。
(A.4.5)でわかる様に![]() は衛星から観測点を見た視線方向の単位ベクトルとなる。また対流圏遅延等を求める際に観測点から見た衛星の方位・仰角の値が必要になるのでその計算も示しておく。観測点から見た衛星の方位・仰角
は衛星から観測点を見た視線方向の単位ベクトルとなる。また対流圏遅延等を求める際に観測点から見た衛星の方位・仰角の値が必要になるのでその計算も示しておく。観測点から見た衛星の方位・仰角![]() は以下により求められる。
は以下により求められる。
ここで方位角![]() は北を
0として時計回りで角度を測る。また
は北を
0として時計回りで角度を測る。また![]() は地球固定座標系から観測点の局地座標系への座標系回転行列、
は地球固定座標系から観測点の局地座標系への座標系回転行列、![]() は局地座標系での衛星位置を示している。局地座標系と衛星方位・仰角の関係を図A.4.2に示す。
は局地座標系での衛星位置を示している。局地座標系と衛星方位・仰角の関係を図A.4.2に示す。
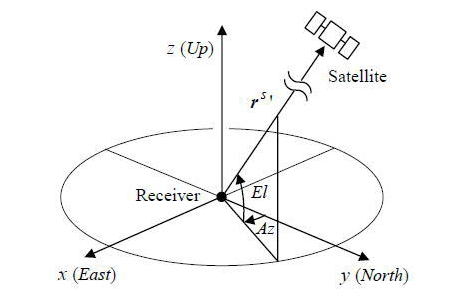
図 A.4.2 局地座標系と衛星方位・仰角
衛星の方位・仰角を求める際に、より精密には光行差 (Aberration)や大気による伝搬経路の曲がりを考慮に入れる場合があるが、GPS/GNSSによる精密測位では通常そこまでの精度は必要としないためここではそれらの効果は無視している。
任意の時刻![]() における衛星位置
における衛星位置![]() 及び衛星時計誤差
及び衛星時計誤差![]() を求めるためには放送暦または精密暦を使用する。
を求めるためには放送暦または精密暦を使用する。
放送暦はGPS/GNSS衛星から送信される測位信号中の航法メッセージに含まれる衛星軌道情報である。放送暦はもともと一般ユーザ向け単独測位用の衛星軌道情報であり、現在の精度は衛星位置で数m、衛星時計誤差で10nsec程度の値である。放送暦は精密測位においても短基線の相対測位に使われることがあるが、長基線の相対測位や精密単独測位に使用するには精度が不足している。放送暦から衛星位置、衛星時計誤差への変換については適当な文献を参照のこと。
精密暦は放送暦に比べてより高精度な衛星軌道情報である。現在最も一般的に使用されている精密暦は IGS(International GNSS Service)が作成・提供しているIGS精密暦であり衛星軌道情報に加えて高精度の衛星時計情報も提供されている。
IGS精密暦は全世界の300局以上の観測局網から得られたデータを使って後処理の精密解析により求められたものであり、インターネットを介して無料で一般に公開されている/2/。準拠する基準座標系はITRF2000であり最新のIGS基準座標系はIGb00と呼ばれる。現在のIGS精密暦は提供タイミングに応じて大きく3つの種類に分けられる。そのうち Ultra-Rapidには決定値に加えて高精度の予報値が含まれているため原理的にはリアルタイムでの利用が可能となる。IGS精密暦の種類を表A.4.1に示す。
| 種類 | Final ( 最終暦) |
Rapid ( 速報暦) |
Ultra-Rapid ( 超速報暦) |
||
|---|---|---|---|---|---|
| 決定 /予報値 | 決定値 | 決定値 | 決定 | 予報 | |
| 時間遅れ | 13 日 | 17 時間 | 3 時間 | 即時 | |
| 提供頻度 | 1 週間毎 | 1 日毎 | 6 時間毎 | ||
| 時間 間隔 |
軌道 | 15 分 | 15 分 | 15 分 | |
| 時計 | 5 分 | 5 分 | 15 分 | ||
| 精度 | 軌道 | <5cm | <5cm | <5cm | 10cm |
| 時計 | <0.1ns | 0.1ns | 0.2ns | 5ns | |
IGS 精密暦以外にもいくつかの各国機関や研究所が独自に決定した高精度の衛星軌道情報を提供しているがIGS精密暦ほど一般的ではない。
さて、精密暦の衛星軌道及び衛星時計情報は放送暦とは異なり一定時間間隔の衛星位置および衛星時計誤差として与えられる。従って任意の時刻の衛星位置及び衛星時計誤差は適当な補間により求める必要がある。
衛星軌道の補間に関しては通常ラグランジェ補間等の多次多項式補間が使われる。 IGS精密暦の15分間隔値であれば、概ね10次以上の多項式を使うことにより十分な精度の補間が可能である。ここで精密暦で与えられる衛星位置は地球固定座標系での衛星重心位置であり衛星アンテナ位相中心オフセットの補正が必要になることに注意する必要がある。詳細はA.4.2.7で再度説明する。
衛星時計誤差の補間に関しては、時計安定度に依存して衛星により異なるが、現在の IGS精密暦の5分間隔または15分間隔値では十分な精度の補間は難しい。従ってより短い時間間隔で解析を行う場合には他のより時間分解能の高い衛星時計情報を使用する必要がある。なお相対測位では後で示すように二重差により衛星時計誤差項を消去して解析するため衛星時計情報は必要とならない。
ここで衛星時計誤差について若干補足する。精密暦の衛星時計誤差は GPS時刻に同期した値が与えられるが、測位計算で必要となるのは測位信号送信時刻の値であり精密暦の時刻とはずれがある。ただし0.1 sec程度の時間内では衛星時計は十分に安定であると考えられるのでその程度の時刻差であれば精密暦を補間した値を使用しても誤差は無視できる。また精密暦の衛星時計誤差からは相対論効果による時計変動が除去されているため、実際の使用にあたってはこの補正を行う必要がある。相対論効果の補正についてはA.4.2.10で説明する。
通常の測位では必要ないが、精密時刻決定等の目的で精密暦を使う場合には精密暦が準拠している時刻系及び時計の定義に注意する必要がある。現在の IGS精密暦が準拠している時刻系は概ねGPS時刻に一致しているが厳密には異なりIGSTまたはIGRTと呼ばれる。また時刻の絶対値決定には擬似距離測定値が使われるが、異なる測位コードの擬似距離測定値間には主にコード間の電子回路遅延差に起因する擬似距離バイアスと呼ぶバイアスが存在するためその補正が必要となる。さらに精密解析で使われる時計誤差は衛星・受信アンテナ位相中心で定義されるため実際の時計とはケーブル遅延、回路遅延分の差がある。精密時刻決定時には以上を十分考慮する必要がある。IGS精密暦が準拠する時刻系の厳密な定義については/3/が詳しい。
ところで衛星の軌道維持のためにしばしば Repositioningと呼ばれる軌道制御が行われることがある。また搭載時計の切り替え等が原因でまれに衛星時計が大きな飛びを起こすことがある。そしてこれらの予期されない現象が発生した場合に放送暦や精密暦予報値の衛星軌道や衛星時計には異常に大きな誤差が含まれる場合があり、その大きさは最大で1000 m以上にも及ぶ。これらの異常値を検出して異常衛星の観測データを除外する等の処置をしないと測位解に大きな誤差を生じることがあるので注意する必要がある。
GPS/GNSS衛星から送信された測位信号の電波は受信機に届くまでに電離層を通過しその影響を受ける。電離層は地球大気上層の分子、原子が太陽光線を受けイオンと電子に電離したもので高度約50〜1000 kmに分布している。
高次項を無視すると、 GPS/GNSSの測位信号で使われるL帯マイクロ波において電離層遅延![]() (m)は以下のように表すことができる。
(m)は以下のように表すことができる。
ここで![]() は搬送波周波数
(Hz)である。
は搬送波周波数
(Hz)である。![]() は電離層に存在する電子密度
は電離層に存在する電子密度![]() を電波伝搬経路に沿って積分した値で総電子数(TEC:
Total Electron Content)と呼ばれTECU=1×1016 electron/m2を単位として表される。(A.4.1),(A.4.2)に示したように電離層遅延
を電波伝搬経路に沿って積分した値で総電子数(TEC:
Total Electron Content)と呼ばれTECU=1×1016 electron/m2を単位として表される。(A.4.1),(A.4.2)に示したように電離層遅延![]() は擬似距離測定においては群遅延としてプラスの影響、搬送波位相測定においては位相が進むことによりマイナスの影響を与えることに注意のこと。電離層の高次項の影響も含めてGPS/GNSSによる測位に対する電離層の影響に関しては/4/が詳しい。
は擬似距離測定においては群遅延としてプラスの影響、搬送波位相測定においては位相が進むことによりマイナスの影響を与えることに注意のこと。電離層の高次項の影響も含めてGPS/GNSSによる測位に対する電離層の影響に関しては/4/が詳しい。
さて(A.4.7)に示したように電離層遅延はほぼ搬送波周波数![]() の二乗に反比例する。従って二周波の搬送波位相に適当な係数を掛けて加算することによりその影響の大部分を消去することができる。この線形結合を電離層フリー線形結合(Ionosphere-Free
Linear Combination)と呼びGPS/GNSSの精密解析において最も重要な基本観測量である。L1、L2搬送波位相の電離層フリー線形結合
の二乗に反比例する。従って二周波の搬送波位相に適当な係数を掛けて加算することによりその影響の大部分を消去することができる。この線形結合を電離層フリー線形結合(Ionosphere-Free
Linear Combination)と呼びGPS/GNSSの精密解析において最も重要な基本観測量である。L1、L2搬送波位相の電離層フリー線形結合![]() (m)の定義と観測モデルを以下に示す。
(m)の定義と観測モデルを以下に示す。
ここで![]() は
L1、L2搬送波位相(m)、
は
L1、L2搬送波位相(m)、![]() はL1、L2搬送波周波数(Hz)、
はL1、L2搬送波周波数(Hz)、![]() はL1、L2搬送波波長(m)、
はL1、L2搬送波波長(m)、![]() はL1、L2搬送波位相バイアス(cycle)、
はL1、L2搬送波位相バイアス(cycle)、![]() は電離層フリー線形結合搬送波位相バイアス(m)、
は電離層フリー線形結合搬送波位相バイアス(m)、![]() は観測誤差 (m)である。長基線の相対測位や精密単独測位では電離層の影響を消去するため電離層フリー線形結合
は観測誤差 (m)である。長基線の相対測位や精密単独測位では電離層の影響を消去するため電離層フリー線形結合![]() を基本観測量として使用することが多い。ただしこの線形結合に含まれる搬送波位相バイアス
を基本観測量として使用することが多い。ただしこの線形結合に含まれる搬送波位相バイアス![]() からはすでに整数性が消えているので二重差をとっても整数とならない。従って相対測位において整数不定性決定が直接は行えないことに注意すべきである。なお電離層フリー線形結合を使用する場合、電離層の高次項による影響は無視することが多いが、最新のより精密な測位においては適当なモデルにより補正を行う場合がある。
からはすでに整数性が消えているので二重差をとっても整数とならない。従って相対測位において整数不定性決定が直接は行えないことに注意すべきである。なお電離層フリー線形結合を使用する場合、電離層の高次項による影響は無視することが多いが、最新のより精密な測位においては適当なモデルにより補正を行う場合がある。
さて一周波の搬送波位相による精密測位や整数不定性決定において電離層遅延をモデルを使って補正する場合があるのでここで紹介しておく。精密測位に一般的に使われる電離層モデルは Single Layerモデルと呼ばれるモデルである。このモデルは電離層を一定高度の単一の薄膜球殻にのみ存在するものと近似し、その電子密度を格子点値や適当な関数で表すものである。この電離層モデルを図A.4.3に示す。
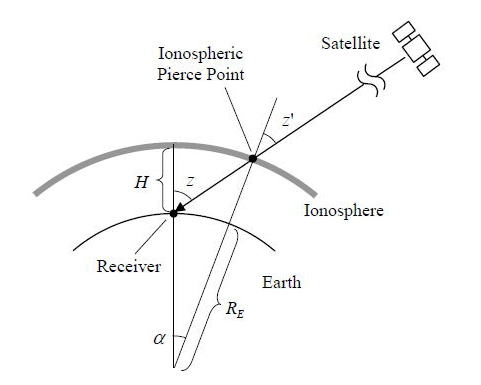
図 A.4.3 Single Layer電離層モデル
このモデルでは衛星から送信された測位信号の電波は高度![]() (m)の電離層を通過し観測点に届く。ここで測位信号が電離層を通過する一点を電離層貫通点(Ionospheric
Pierce Point)と呼ぶ。観測点の緯度・経度を
(m)の電離層を通過し観測点に届く。ここで測位信号が電離層を通過する一点を電離層貫通点(Ionospheric
Pierce Point)と呼ぶ。観測点の緯度・経度を![]() ,
,![]() 、観測点から見た衛星の方位・仰角を
、観測点から見た衛星の方位・仰角を![]() 、地球半径を
、地球半径を![]() (m)として、電離層貫通点の緯度・経度
(m)として、電離層貫通点の緯度・経度![]() ,
,![]() 及び電離層貫通点での衛星方向天頂角
及び電離層貫通点での衛星方向天頂角![]() は以下で求められる。なおここでは地球は球に近似している。
は以下で求められる。なおここでは地球は球に近似している。
![]()
![]()
![]()
![]()
![]()
時刻![]() 、緯度・経度
、緯度・経度![]() ,
,![]() における、電離層の垂直総電子数(VTEC: Vertical
TEC)が関数
における、電離層の垂直総電子数(VTEC: Vertical
TEC)が関数![]() (TECU)で与えられるものとして電離層遅延
(TECU)で与えられるものとして電離層遅延![]() (m)は以下で求められる。
(m)は以下で求められる。
電離層の状態は、太陽活動、季節、時間帯、緯度などの条件によって大きく変動するため、電離層の電子密度分布の精密な予測は難しい。従って垂直総電子数![]() は電離層の精密観測により別途推定された値を使用する。通常これらの推定値は一定時間間隔の格子点値または球面調和関数等の適当な関数の係数として与えられるのでこれを時間補間、位置補間して利用する。
は電離層の精密観測により別途推定された値を使用する。通常これらの推定値は一定時間間隔の格子点値または球面調和関数等の適当な関数の係数として与えられるのでこれを時間補間、位置補間して利用する。
電離層モデルのうち全地球的な電離層の状態を表すものは GIM(Global Ionosphere Maps) と呼ばれる。より空間分解能が高く領域の狭いものはLIM(Local Ionosphere Maps)と呼ばれ一般にGIMより高精度の補正が可能である。
GIMの例としてIGSが提供している電離層モデルを図A.4.4に示す。この例では2時間間隔の垂直総電子数が緯度2.5度、経度5度間隔の格子点値として与えられる。ただし、これらの補正モデルで得られる精度は、二周波搬送波位相の電離層フリー線形結合による補正精度より低いのが普通である。例えばIGS電離層モデルの公称精度は2-8 TECUでありL1天頂電離層遅延に換算すると0.3〜1.3m程度の精度しかない。
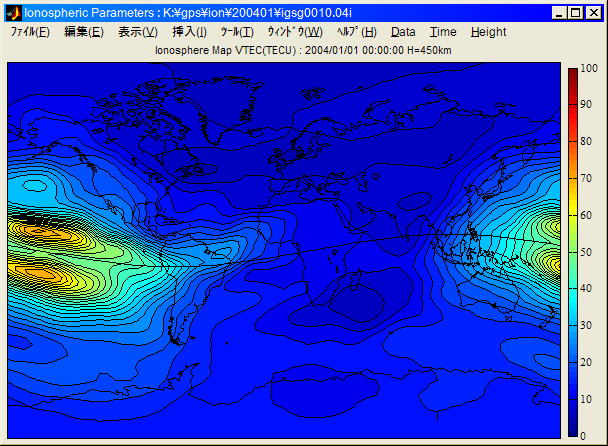
図
A.4.4 電離層モデルの例(VTEC)
(IGS TEC 2004/1/1 00:00 H=450km,
単位:TECU)
対流圏遅延は測位信号の電波が大気中を通過することにより真空中より減速する効果と伝播経路がわずかな曲率を持つため直線から延びる効果からなる。対流圏遅延は乾燥大気による遅延である静水圧遅延と大気中の水蒸気による遅延である湿潤遅延に分けられ、その大きさとしては天頂方向の静水圧遅延で 2.0〜2.4 m、湿潤遅延で0〜40 cm程度の値となる。また概ね仰角のsinに反比例する性質を持つ。
対流圏遅延を![]() (m)として、精密測位で使われる一般的な対流圏遅延モデルを以下にに示す。
(m)として、精密測位で使われる一般的な対流圏遅延モデルを以下にに示す。
ここで![]() ,
,![]() はそれぞれ天頂静水圧遅延(m)、天頂湿潤遅延(m)を表している。また
はそれぞれ天頂静水圧遅延(m)、天頂湿潤遅延(m)を表している。また![]() はそれぞれ静水圧遅延、湿潤遅延のマッピング関数であり、遅延量の衛星仰角
はそれぞれ静水圧遅延、湿潤遅延のマッピング関数であり、遅延量の衛星仰角![]() に対する依存性を表す関数である。
に対する依存性を表す関数である。
対流圏遅延のうち天頂静水圧遅延![]() (m)は地上気圧を与えることにより以下に示すモデルにより高い精度で求めることができる。
(m)は地上気圧を与えることにより以下に示すモデルにより高い精度で求めることができる。
ここで![]() ,
,![]() はそれぞれ観測点の緯度及び高度 (m)である。
はそれぞれ観測点の緯度及び高度 (m)である。![]() は地上気圧 (hPa)であり気象観測値により与える。地上気圧の直接の観測値が得られない場合、近隣点の観測値や数値予報モデル等を使う場合があるが地上気圧は高度に大きく依存するのでその補正を忘れてはならない。なお地上気圧は簡易に標準的な大気モデルで代替することも多い。例としてICAO標準大気モデルを使って求める場合を以下に示す。
は地上気圧 (hPa)であり気象観測値により与える。地上気圧の直接の観測値が得られない場合、近隣点の観測値や数値予報モデル等を使う場合があるが地上気圧は高度に大きく依存するのでその補正を忘れてはならない。なお地上気圧は簡易に標準的な大気モデルで代替することも多い。例としてICAO標準大気モデルを使って求める場合を以下に示す。
![]()
ここで高度は厳密にはジオポテンシャル高度で定義されるが測地高度や回転楕円体高で代替しても問題はない。標準大気モデルを使う場合、天頂静水圧遅延としては最大数 cmの誤差を生じるが、以下に示すように湿潤遅延または全遅延を未知パラメータとして推定する場合にはそちらにその誤差が吸収されるため全遅延としてはほとんど補正精度の劣化はない。
湿潤遅延は一般には地上観測値とアプリオリなモデルを使って十分な精度で求めることができない。これは対流圏内の水蒸気分布が空間的な局所性を持っており、地上観測値は必ずしもその状態を反映していないためであると考えられている。そこで精密測位では、測位計算と同時に天頂湿潤遅延![]() を未知パラメータとしてその値を推定することが多い。湿潤遅延は時間によって変動するので一定の時間間隔で適当な時間相関を仮定した確率論モデルを使ってその値を推定する。なお静水圧遅延を標準大気モデルを使って計算する場合などには
を未知パラメータとしてその値を推定することが多い。湿潤遅延は時間によって変動するので一定の時間間隔で適当な時間相関を仮定した確率論モデルを使ってその値を推定する。なお静水圧遅延を標準大気モデルを使って計算する場合などには![]() の代わりに天頂全遅延
の代わりに天頂全遅延![]() を未知パラメータに選ぶ場合がある。
を未知パラメータに選ぶ場合がある。
マッピング関数については過去多数の研究があるが、現在の精密測位で最も一般的に使われているものは
NMF /5/ である。これは以下の様に仰角![]() と係数
と係数![]() を使った連分数の形で関数を表すものである。
を使った連分数の形で関数を表すものである。
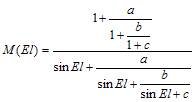
ここで係数![]() は静水圧遅延、湿潤遅延毎に係数テーブルと観測点緯度、高度、通算日を使って求める。これらの係数は多数の観測データと数値シミュレーションで求められたものである。
NMFでは気象観測データの入力なしに仰角3度までの関数値が十分な精度で計算することができるとされており、その使いやすさから現在の精密解析では標準的なマッピング関数となっている。
は静水圧遅延、湿潤遅延毎に係数テーブルと観測点緯度、高度、通算日を使って求める。これらの係数は多数の観測データと数値シミュレーションで求められたものである。
NMFでは気象観測データの入力なしに仰角3度までの関数値が十分な精度で計算することができるとされており、その使いやすさから現在の精密解析では標準的なマッピング関数となっている。
一般的なマッピング関数では対流圏遅延の水平方向の等方性を仮定しているが、実際の大気では水平方向の異方性を持っておりこれらの補正により特に海沿いの地方等の気象条件が方位により異なる観測点の水平方向の測位精度向上がはかれると言われている。この目的で対流圏遅延モデルに水平勾配項を追加しそのパラメータを推定する場合や仰角に加え方位角をパラメータにしたマッピング関数を使用する場合がある。
対流圏遅延の補正残差は精密測位において大きな誤差要因のひとつであり測位精度向上のため色々な研究が成されている。数値気象予報モデルのデータを使って補正を行う方法や特別な例ではあるが水蒸気ラジオメータと呼ぶ視線方向の水蒸気量を測定する計測器を使って大気の水蒸気量を計測しその結果で補正を行う方法もある。精密測位における対流圏遅延の影響、マッピング関数や対流圏遅延パラメータの推定手法については /6/に詳しい。
アンテナ位相中心とは電波の発射、入射において仮想的に電波の集中点と見なせる点である。理想的なアンテナではこの点は一点に定まるが現実のアンテナでは電波の発射、入射方向に依存して変動する。従って現実のアンテナではアンテナ位相中心は空間上の全方向から見たアンテナ位相中心の平均位置として定義する。そしてアンテナ位相中心を基準にした方向に依存した変動成分をアンテナ位相中心変動 (PCV: Phase Center Variation)と呼ぶ。
受信アンテナ位相中心の物理的な位置関係を図
A.4.5に示す。アンテナ底面等の物理的に決められたアンテナ基準点(ARP)から測ったアンテナ位相中心位置をアンテナ位相中心オフセットと呼ぶ。地球固定座標系での測位基準点の位置を![]() (m)とすると受信アンテナ位相中心位置
(m)とすると受信アンテナ位相中心位置![]() (m)は以下のように表せる。
(m)は以下のように表せる。
ここで![]() は観測点の局地座標系で表した受信アンテナ位相中心オフセット及び測位基準点を基準としたアンテナ基準点位置ベクトル
(m)、
は観測点の局地座標系で表した受信アンテナ位相中心オフセット及び測位基準点を基準としたアンテナ基準点位置ベクトル
(m)、![]() は地球固定座標系から観測点の局地座標系への座標系回転行列である。
は地球固定座標系から観測点の局地座標系への座標系回転行列である。
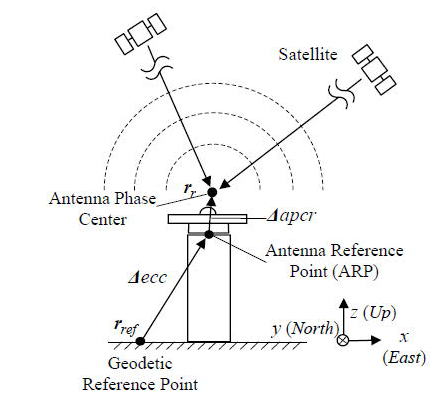
図 A.4.5 受信アンテナ位相中心の位置関係
受信アンテナ位相中心変動が衛星方位・仰角![]() の関数
の関数![]() (m)で表されるとして受信アンテナ位相中心変動補正
(m)で表されるとして受信アンテナ位相中心変動補正![]() (m)は以下のように書ける。
(m)は以下のように書ける。
さてこれらのアンテナ位相中心オフセット、アンテナ位相中心変動のパラメータはアンテナメーカや関連機関が地上における精密測定で決定した標準的な値を使用することが多い。これらのパラメータはアンテナ機種毎のテーブルの形で提供される。アンテナ位相中心変動 (PCV)テーブルの例を図A.4.6に示す。
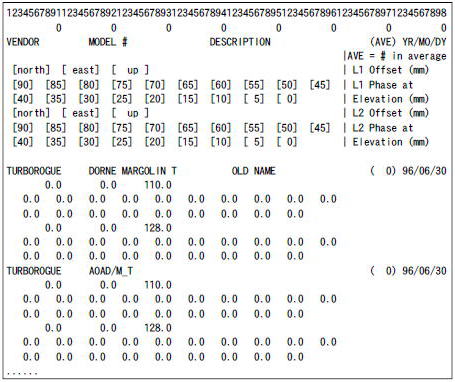
図 A.4.6 アンテナ位相中心変動(PCV)テーブルの例
(IGS 標準アンテナPCVテーブルIGS_01.PCV,一部)
この例では L1、L2それぞれについてアンテナ位相中心オフセット及び仰角5度毎のアンテナ位相中心変動の値が与えられている。なおこれらのパラメータは通常L1、L2毎に与えられるので搬送波位相の線形結合を測位に使用する場合はこれらのパラメータも同一係数を使った線形結合の値を使用する必要がある。
アンテナ位相中心位置やアンテナ位相中心変動の値は同一機種のアンテナを使ってもその設置環境に影響を受けると言われており、例えばレドームと呼ぶアンテナカバー、アンテナ設置構造物、積雪等による影響が報告されている。特に精度が要求される場合は設置環境でアンテナ特性の精密計測を行ったり、長期の観測データから統計処理によりアンテナ位相中心変動の係数を求め補正を行う場合がある。
精密暦における衛星位置は衛星重心位置で表される。従って衛星アンテナ位相中心位置を求めるためには衛星アンテナ位相中心オフセットの補正が必要となる。
地球固定座標系での衛星重心位置を![]() (m)、衛星固定座標系での衛星アンテナ位相中心オフセットを
(m)、衛星固定座標系での衛星アンテナ位相中心オフセットを![]() (m)、衛星固定座標系から地球固定座標系への座標系回転行列を
(m)、衛星固定座標系から地球固定座標系への座標系回転行列を![]() として地球固定座標系での衛星アンテナ位相中心位置
として地球固定座標系での衛星アンテナ位相中心位置![]() は以下で与えられる。
は以下で与えられる。
衛星アンテナ位相中心オフセットの値については必ずしも標準的なものは存在しないが、 IGSが現在標準的な解析に採用している値を例として表A.4.2に示す。衛星アンテナ位相中心変動についても受信アンテナと同様に補正を行う場合があるがあまり一般的でないのでここでは省略する。
| 衛星 | アンテナ位相中心オフセット (m) | ||
|---|---|---|---|
| x | y | z | |
| GPS Block II/IIA | 0.279 | 0.000 | 1.023 |
| GPS Block IIR | 0.000 | 0.000 | 0.000 |
さて衛星アンテナ位相中心オフセットに関連して GPS/GNSS測位におけるGlobal Scale Offsetの問題につき簡単に触れておく。VLBI、SLR等他の精密宇宙測位技術で決定された座標に比較して、GPSによる精密測位解には上下方向で数cmのグローバルな系統オフセットが見られることが以前から指摘されている。これらオフセットの原因は必ずしも明確になっていないが解析に使用する衛星アンテナ位相中心オフセットの値が十分に校正されたものでないことが原因の一つとして有力視されている。
これらの問題に対応するため座標値の定まった全世界の基準点の測位結果から求めた係数を使って測位解を補正する場合がある。また IGSにおいてもこれらのグローバルオフセットの問題を解消するため解析に使う標準的なアンテナ位相中心パラメータを精密に校正されたものに変更するという動きがある。
月や太陽の引力の影響で地球がわずかに弾性変形を起こす現象を地球潮汐と呼ぶ。地表に固定された観測点は地球潮汐の影響で周期的な変動を起こす。この変動を局位置変動 (Site Displacement) と呼ぶ。
近年の VLBI, SLR, GPS等の宇宙測地技術の発達により、地球潮汐の効果が高精度に測定され精密な潮汐モデルが作られて来た。それによると地球潮汐による地上観測点の局位置変動は大きい地点で上下方向最大20 cmにも及ぶ。固定観測点の精密測位を行う場合、測位精度に比較しこれらの影響が十分に大きいのでこれらの変動を補正する必要がある。
地球潮汐は幾つかの要素から構成されるが主なものは固体地球潮汐 (Solid Earth Tide), 海洋荷重(Ocean Loading) 、極運動潮汐(Pole Tide)である。その他、大気荷重(Atmospheric Loading) や積雪加重(Snow Loading)による位置変動も報告されている。地球潮汐による精密な局位置変動モデルについては/7/, /8/が詳しい。これらの文献で示される最新の地球潮汐モデルでは変動成分としてmm以下の項まで考慮されており、計算も大変に複雑であるが、補正に当たっては必要な精度に応じて主要項のみ考慮すればよい。なおITRF等の基準座標系を構成する基準点の座標はこれらの局位置変動を除去した値として定義されるのが一般的である。地球潮汐による局位置変動の例として精密モデルで求めた筑波の位置変動を図A.4.7に示す。
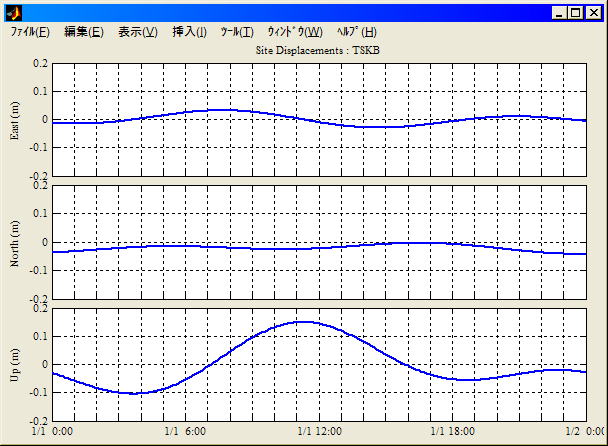
図 A.4.7 精密モデルで求めた局位置変動の例
(2004/1/1 0:00 〜1/2 0:00UTC 筑波)
局位置変動を含まない地球固定座標系での観測点の位置を![]() 、観測点における地球潮汐による局位置変動の東、北、上方向成分をそれぞれ
、観測点における地球潮汐による局位置変動の東、北、上方向成分をそれぞれ![]() (m)、地球固定座標系から観測点の局地座標系への座標系回転行列を
(m)、地球固定座標系から観測点の局地座標系への座標系回転行列を![]() として局位置変動補正後の観測点位置
として局位置変動補正後の観測点位置![]() は以下の様に表される。
は以下の様に表される。
GPS衛星から送信される測位信号搬送波の偏波は右旋円偏波であり衛星アンテナと受信アンテナの相対的な位置関係が回転することにより受信した搬送波の位相が進んだり遅れたりする効果を及ぼす。これをPhase
Wind-up効果と呼ぶ。衛星アンテナ、受信アンテナの有効ダイポールベクトルを![]() として相対アンテナ回転角
として相対アンテナ回転角![]() (rad)は以下の様に表される。
(rad)は以下の様に表される。
![]()
![]()
![]()
![]()
ここで![]() は衛星固定座標系
は衛星固定座標系![]() 軸方向単位ベクトル、
軸方向単位ベクトル、![]() は観測点の局地座標系
は観測点の局地座標系![]() 軸方向単位ベクトル、
軸方向単位ベクトル、![]() は衛星から観測点を見た視線方向単位ベクトルを表す。時刻
は衛星から観測点を見た視線方向単位ベクトルを表す。時刻![]() における相対アンテナ回転角をそれぞれ
における相対アンテナ回転角をそれぞれ![]() として時刻
として時刻![]() から
から![]() までの衛星運動による
Phase Wind-up効果
までの衛星運動による
Phase Wind-up効果![]() (m)は以下の様に表される。
(m)は以下の様に表される。
GPS衛星では通常アンテナ面が地心方向、太陽電池パドル面が太陽方向と垂直になる様に姿勢制御されており、軌道運動と共に衛星−地心を結ぶ軸を中心に緩やかに回転している。しかし衛星が地球の影(食)に入ると姿勢制御モードが変わり、特にGPS Block II/IIA衛星では太陽捕捉のため通常より高速に回転を始め、衛星が食から出て太陽を再捕捉するまでこの高速回転が続くと言われている。この期間ではPhase Wind-up効果が通常より大きくなり、通常の衛星姿勢を前提にしたモデルでは最大で10 cm程度の誤差を生じる。
またこの期間には衛星アンテナ位相中心位置のモデルにも誤差が生じるし、食時の衛星にはモデル化困難な擾乱要素が加わり精密暦の衛星軌道推定誤差も大きいと考えられるため、精密測位では食時の衛星の観測データを使用しない、あるいは重みを下げて使用する等の対策を行うことがある。
特殊相対論の効果により衛星搭載時計には遅れが生じる。衛星の軌道が正確な円軌道の場合にはこの値は一定値になるが、実際の衛星軌道の離心率は 0ではないため、衛星軌道周回に同期した周期的な変動をもたらす。その大きさは軌道の離心率が大きい衛星で10m以上にも達することがある。
精密暦から得られる衛星時計誤差にはこの相対論効果による変動が除去されているため使用にあたってはこの補正を行う必要がある。相対論効果補正前の衛星時計誤差を![]() (sec)、衛星位置(m)及び速度(m/sec)をそれぞれ
(sec)、衛星位置(m)及び速度(m/sec)をそれぞれ![]() として補正後の衛星時計誤差
として補正後の衛星時計誤差![]() は以下で表される。
は以下で表される。
ここで衛星速度は慣性空間上での速度を表すことに注意のこと。従って衛星速度が地球固定座標系で与えられる場合には地球回転による速度分を加算する必要がある。
その他、地球重力場による一般相対論効果により電波伝搬経路に曲がりが生じるとされ、その電波伝搬距離が伸びる効果の補正を行うことがあるが、この影響はわずかのため通常は無視することが多い。
マルチパスは衛星から送信された測位信号が受信機近くの物体に反射され伝搬経路が複数となることにより電波伝搬時間に変動を起こす現象である。マルチパスは擬似距離測定値においては大きな誤差要因であり大きな場合でその大きさは数 mに達することがある。搬送波位相測定値においても擬似距離測定値と同様にマルチパスの影響を受けるがその大きさは擬似距離に比べるとずっと小さく、マルチパス対策を施した精密測位用のアンテナ及び受信機を使用した場合では最大でも数cmのオーダーである。厳密に言えばマルチパスとA.4.2.6で説明した受信アンテナ位相中心変動とを区別するのは難しいが衛星方位・仰角に依存した高周波の変動成分をマルチパス、低周波の変動成分を受信アンテナ位相中心変動と呼ぶことが多い。マルチパスを特別な数値モデルにより補正したり、GPS衛星では約23時間56分周期で観測点から見た衛星方向がほぼ同一のパスを通ることを利用して過去の観測データとの相関を使って補正したりすることもあるが、一般には観測誤差の一部として扱うことが多い。
最新の GPS/GNSS受信機の搬送波位相測定における受信機雑音は通常数mm以下と言われているが、一部の受信機では電離層擾乱時に雑音が大きくなるものがある等、実際の受信機雑音の大きさは使用する受信機に大きく依存する。その他電離層遅延・対流圏遅延の補正残差もモデル化が難しく、マルチパス、受信機雑音、電離層遅延・対流圏遅延補正残差等unknownなファクターを合計して観測誤差として扱うことが多い。
一般にこれらの観測誤差の大きさは低仰角で大きくなり観測データの品質が悪化するため一定の仰角未満の観測データは解析に使用しない様にすることが多い。この仰角をカットオフ角と呼び通常10〜15度に設定する。
また観測誤差の大きさを仰角に依存した経験的なモデルで表し低仰角の観測データの重みを下げることが行われる。観測誤差標準偏差を![]() (m)、天頂観測誤差標準偏差を
(m)、天頂観測誤差標準偏差を![]() (m)、衛星仰角を
(m)、衛星仰角を![]() として表した観測誤差モデルの例を以下に示す。なおこれらのモデルは通常精密解析ソフト毎に異なることが多く標準的なモデルと言えるものは存在しない。
として表した観測誤差モデルの例を以下に示す。なおこれらのモデルは通常精密解析ソフト毎に異なることが多く標準的なモデルと言えるものは存在しない。
![]()
二周波受信機において同時に測定した二周波測位信号の擬似距離または搬送波位相に定数を掛けて足し合わせて見かけ上新しい測定値を生成することができる。この測定値を線形結合 (Linear Combination)と呼ぶ。
精密測位においては測定値に含まれる特定のモデル項を強調したり消去したりして解析を容易にする目的で、色々な場面でこの線形結合を使用する。精密測位で使用される主な線形結合を表
A.4.3に示す。表中には波長、![]() を基準とした電離層遅延の影響、観測誤差の大きさも示している。
を基準とした電離層遅延の影響、観測誤差の大きさも示している。
| 記号 | 線形結合 | 波長 (cm) |
電離層 | 誤差 (cm) |
|---|---|---|---|---|
| L1 | (L1 搬送波位相) | 19.0 | 1.0 | 0.3 |
| L2 | (L2 搬送波位相) | 24.4 | 1.6 | 0.3 |
| LC | 電離層フリー | - | 0.0 | 0.9 |
| LG | 幾何学フリー | - | 0.6 | 0.4 |
| WL | ワイドレーン | 86.2 | 1.3 | 1.7 |
| NL | ナローレーン | 10.7 | 1.3 | 1.7 |
| MW | Melbourne-Wübbena | 86.2 | 0.0 | 21 |
| MP1 | L1 マルチパス | - | 0.0 | 30 |
| MP2 | L2 マルチパス | - | 0.0 | 30 |
表 A.4.3で示した各線形結合の具体的な定義とその観測モデルを以下に示す。
![]()
![]()
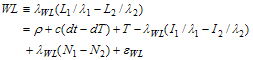
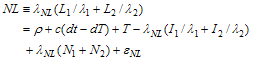
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ここで![]() はそれぞれ
L1、L2擬似距離及び搬送波位相測定値(m)を示す。また
はそれぞれ
L1、L2擬似距離及び搬送波位相測定値(m)を示す。また![]() はそれぞれL1、L2搬送波周波数(Hz)及び波長(m)、
はそれぞれL1、L2搬送波周波数(Hz)及び波長(m)、![]() は幾何学距離(m)、
は幾何学距離(m)、![]() はそれぞれ受信機及び衛星時計誤差(sec)、
はそれぞれ受信機及び衛星時計誤差(sec)、![]() はそれぞれL1、L2電離層遅延、
はそれぞれL1、L2電離層遅延、![]() はそれぞれL1、L2搬送波位相バイアス、
はそれぞれL1、L2搬送波位相バイアス、![]() は各線形結合の観測誤差(m)である。
は各線形結合の観測誤差(m)である。
これらの線形結合のうち電離層フリー線形結合![]() については既にA.4.2.4で説明した。なお
については既にA.4.2.4で説明した。なお![]() は
は![]() と表記することもある。幾何学フリー線形結合
と表記することもある。幾何学フリー線形結合![]() は幾何学距離、衛星時計誤差、受信機時計誤差の項が消去され電離層遅延項と搬送波位相バイアスによる定数項のみが残るため高精度の電離層観測やサイクルスリップ検出・修正に使われる。ワイドレーン、ナローレーン線形結合
は幾何学距離、衛星時計誤差、受信機時計誤差の項が消去され電離層遅延項と搬送波位相バイアスによる定数項のみが残るため高精度の電離層観測やサイクルスリップ検出・修正に使われる。ワイドレーン、ナローレーン線形結合![]() は主に相対測位における整数不定性決定に使用される。Melbourne-Wübbena線形結合
は主に相対測位における整数不定性決定に使用される。Melbourne-Wübbena線形結合![]() は幾何学項、電離層項が消去されかつ波長が長いため整数不定性決定やサイクルスリップの検出、修正に使用される。L1、L2マルチパス
は幾何学項、電離層項が消去されかつ波長が長いため整数不定性決定やサイクルスリップの検出、修正に使用される。L1、L2マルチパス![]() は定数項以外はL1、L2擬似距離観測誤差のみが残るためほぼ擬似距離マルチパスの相対的な大きさを表す。従って擬似距離マルチパスの解析やサイクルスリップ検出に使用される。
は定数項以外はL1、L2擬似距離観測誤差のみが残るためほぼ擬似距離マルチパスの相対的な大きさを表す。従って擬似距離マルチパスの解析やサイクルスリップ検出に使用される。
なお、これらの線形結合を作ることによりオリジナルの測定量に比較して観測誤差が増大することに注意しなければならない。線形結合による観測誤差の増大を避けるためオリジナルの測定量をそのまま精密測位に使用する場合もある。
| A.4.1 はじめに← | →A.4.3 パラメータ推定の手法 |
| Copyright (C) 2005 by Tomoji Takasu, All rights reserved |