A.4.4　相対測位
A.4.4.1　二重差
A.4.4.2　相対測位の手法
A.4.4.3　整数不定性決定
A.4.4.4　相対測位の応用

A.4.4　相対測位

相対測位は搬送波位相測定値を使った最も一般的な精密測位法であり、搬送波位相の二重差を基本観測量として推定を行う。相対測位は干渉測位または基線解析と呼ばれることもある。以下に相対測位の原理と手法を説明する。

A.4.4.1　二重差

図A.4.8で示すように2つの観測点でほぼ同時に測定した衛星の搬送波位相をそれぞれとする。ここで上付文字が衛星、下付文字が観測点を示すものとし以下の他の項でも同様とする。

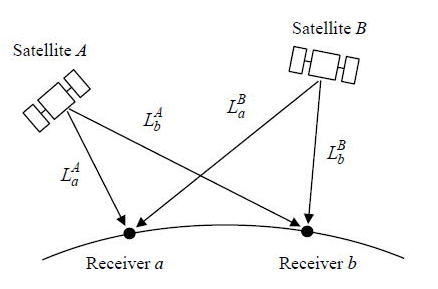
図 A.4.8　2観測点での搬送波位相の測定

これらから搬送波位相二重差を以下のように定義する。

ここで二重上付文字は衛星間、二重下付文字は観測点間で差をとることを示すものとし、他の項でも同様とする。(A.4.2)を使うと搬送波位相二重差の観測モデルは以下の様に書ける。

各受信機において搬送波位相は同時測定されることを考慮すると、

となる。また測位信号の衛星送信時刻がほぼ同時で短い時間内では衛星時計は十分安定であることを考慮すると、

と書ける。また (A.4.3)を使うことにより、

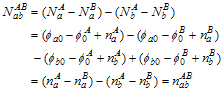
となることに注意すると最終的に搬送波位相二重差の観測モデルは以下で表すことができる。

(A.4.21)

以上のように、搬送波位相二重差からは衛星時計誤差、受信機時計誤差項が消去されていることが分かる。また搬送波位相バイアスの衛星初期位相、受信機初期位相の項も消去され、整数不定性 (Integer Ambiguity)のみ残るため搬送波位相バイアスの二重差は整数となる。

さて相対測位において 2つの観測点間のベクトルを基線(Baseline)と呼ぶ。ここで基線が十分に短い、すなわち観測点が地理的に十分近い場合を考える。十分近い2つの観測点からほぼ同一時刻に同一衛星を観測した場合、電離層遅延、対流圏遅延はほぼ同一の値になることが期待できる。すなわち、

,,,

と近似でき、最終的に搬送波位相二重差は以下に示すような簡単な形で書くことができる。

(A.4.22)

相対測位では以上に示した搬送波位相二重差を基本観測量に使用することにより、取扱いの難しいパラメータを観測モデルから消去して推定を容易にしている。

A.4.4.2　相対測位の手法

以下に相対測位の手法を説明する。ここではパラメータ推定に最小二乗法を使用する。

十分に短い基線を考える。地球固定座標系での観測点の位置をとして単独測位等を使ってその概略値がで与えられるものとする。また観測点を基準観測点としその位置は十分な精度で既知であるとする。

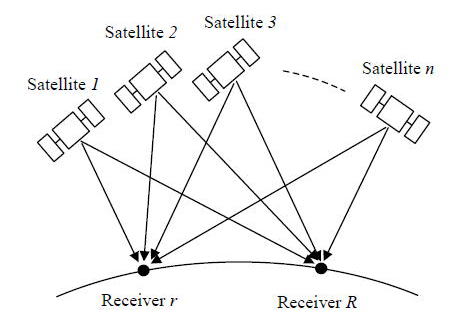
図 A.4.9　相対測位の概念図

観測点で一定期間衛星の搬送波位相を測定しその観測データが得られたとする。観測期間中にサイクルスリップは発生しないと仮定するとこの期間内で搬送波位相バイアス二重差は一定の値になる。従って、ここで未知パラメータおよびその近似解を以下と置く。

観測期間中の観測時刻において測定した搬送波位相の二重差により観測量ベクトル

を作る。ここで観測量間の線形独立性を確保するため、衛星に関しては、任意の基準衛星を1つ決めて基準衛星と他の衛星の間でのみ差をとることにする。ここでは衛星1を基準衛星としている。

さてと置いた時の観測モデル、計画行列及び観測誤差共分散行列は(A.4.22)を使って以下の様に表すことできる。

( ,)

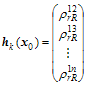
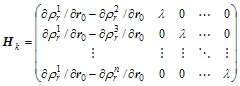
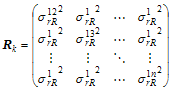
ここでは観測点の位置をとして計算した衛星との幾何学距離、は観測誤差の標準偏差である。観測期間中の観測時刻をとすると、全観測量、観測モデル、計画行列及び重み行列は、

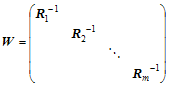
と書くことができる。これらに(A.4.18)で示した最小二乗法による推定を適用することにより、未知パラメータの最小二乗推定値、すなわち観測点の位置及び搬送波位相バイアス二重差の推定値を求めることができる。

以上は観測期間中観測点の位置が一定である場合すなわちスタティック測位の場合であった。観測点の位置が可変すなわちキネマティック測位の場合は観測点の位置を観測時刻毎に独立の未知パラメータと置く。すなわち

と置き同様の推定を行うことにより移動体の位置が求められる。

以上、単純化した相対測位の手法を説明した。実際の観測データでは観測期間中に衛星が切り替わったり、サイクルスリップが発生したりしてそれらの考慮が必要になるためより処理が複雑となる。またここでは基線が十分短く電離層遅延、対流圏遅延の影響を無視できる場合を示したが、より長い基線では(A.4.21)に示したように電離層遅延、対流圏遅延の影響を無視できないためそれらの補正が必要となる。また相対測位では受信アンテナ位相中心、局位置変動、Phase Wind-up等の誤差要因の影響も二重差をとることにより消去または軽減されるため補正を省略することが多いが、より精度が必要な解析の場合には先に説明したモデルを使って補正を行う必要がある。

なお以上は単一基線を使って単一観測点位置を求める相対測位の例であったが実際の解析では複数基線を使って複数観測点の測位を行う様な複雑な場合もある。ただし基本は今まで説明した手法と変わりはない。

A.4.4.3　整数不定性決定

前項で説明した手順により観測点の位置と搬送波位相バイアス二重差の推定値が得られた。ここで得られた搬送波位相バイアス二重差の推定値は一般には実数であり、同時に得られた測位解は FLOAT解と呼ばれる。

A.4.4.1で示したように搬送波位相バイアス二重差は整数となるが、この整数条件を利用して適当な統計的な妥当性を仮定し推定値を整数に固定することにより測位解の精度を改良することが行われる。これを整数不定性(Integer Ambiguity)を決定する、解く、あるいはfixすると言い最終的に得られた測位解はFIX解と呼ばれる。

相対測位における整数不定性決定の効率化、高速化や高信頼性化は精密測位技術における主要課題のひとつであり、過去の多数の研究により各種の手法が考案されてきた。整数不定性決定の手法は本稿の範囲外であり詳細は説明しない。適当な文献を参照のこと。

A.4.4.4　相対測位の応用

相対測位の応用として重要な技術をいくつか簡単に紹介する。

(1) RTK( リアルタイムキネマティック)

RTKは、基準観測点の測定データを無線等を使ってリアルタイムで移動観測点に送信し、観測点の搬送波位相測定値と送信された基準観測点の測定値を使って相対測位により移動観測点位置をリアルタイムで精密測定する技術である。

通常は移動開始前に初期化と呼ぶ整数不定性を解く操作を行ってから測定開始するが移動中に整数不定性を解く技術も開発されている。

(2) 仮想基準点

仮想基準点は、地上基準観測点網の観測データから擬似的な基準観測点での測定値を生成し移動観測点に送信し、その観測データを使って相対測位により移動観測点の位置を精密測定する技術である。ユーザが基準観測点を用意する必要がない、初期化時間を短縮できる等のメリットがある。サービス提供者により擬似測定値の生成方法等が異なる幾つかの方式がある。