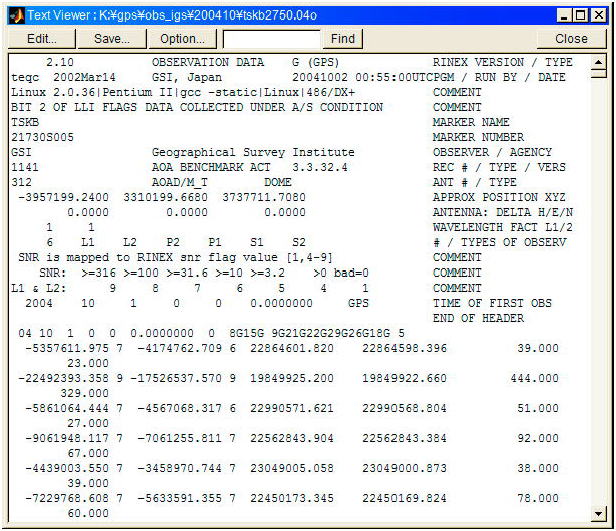
図 A.4.11 RINEX観測データ例(一部)
|
搬送波位相測定値による精密測位の理論及び解析処理 |
Home |
A.4.6 精密解析の実際
A.4.6.1 観測データ
A.4.6.2 観測データの編集
A.4.6.3 単独測位による概略値計算
A.4.6.4 受信機時計飛びの検出と修正
A.4.6.5 サイクルスリップの検出と修正
A.4.6.6 パラメータ推定
A.4.6.7 アウトライアの検出と除去
A.4.6.8 精密解析の例
以下に実際の精密解析の手法につき流れを追って説明し具体的な解析例についても示す。ここでは後処理解析の例を示しておりリアルタイム解析では状況が異なる点が多いことに注意のこと。なお以下で示す図はすべて現在筆者が開発中の精密解析ソフトウェア GpsTools(GT)/10/により出力した画面である。
GPS/GNSSの観測データ、精密暦、解析結果、パラメータデータ等には国際的な標準形式が定められているため、精密解析でもそれらの形式のデータを使用することが多い。精密解析で使用する主な標準データ形式を表A.4.5に示す。
| データ種別 | 標準データ形式 | |
|---|---|---|
| 観測データ | RINEX OBS | |
| 航法メッセージ | RINEX NAV | |
| 気象観測データ | RINEX MET | |
| 精密暦 | 衛星軌道・時計 | NGS SP3, SP3c |
| 衛星・観測局時計 | RINEX CLK | |
| 測位解析結果 | SINEX | |
| 電離層モデル | IONEX | |
これらのうち観測データは RINEXと呼ぶ形式で取り扱われるのが普通で大部分の精密解析ソフトウェアがサポートしている。また多くの精密測位用GPS/GNSS受信機は観測データをRINEX形式として出力できるか、または受信機独自形式からRINEX形式への変換ユーティリティを持っている。RINEX観測データはテキスト形式のファイルだが保存サイズを削減するため圧縮ファイルとして扱うこともある。この際一般的な圧縮形式であるcompress, gzip形式やHatanaka-Compressionと呼ぶRINEX専用の高効率圧縮形式が使われる。
RINEX観測データの例を図A.4.11に示す。RINEX観測データのヘッダ部には受信機機種名、受信アンテナ名、観測点概略位置、受信アンテナ偏心ベクトル等の情報が含まれる。観測データ本体部には観測時刻、観測衛星リスト及び擬似距離及び搬送波位相測定値が含まれる。観測データ本体部には信号強度、ドップラーシフト等の測定値が含まれる場合がある。
観測時に同時に得られた航法メッセージ、気象観測データも RINEX航法メッセージ形式、RINEX気象観測データ形式で格納され後の精密解析に使用される。

図
A.4.11 RINEX観測データ例(一部)
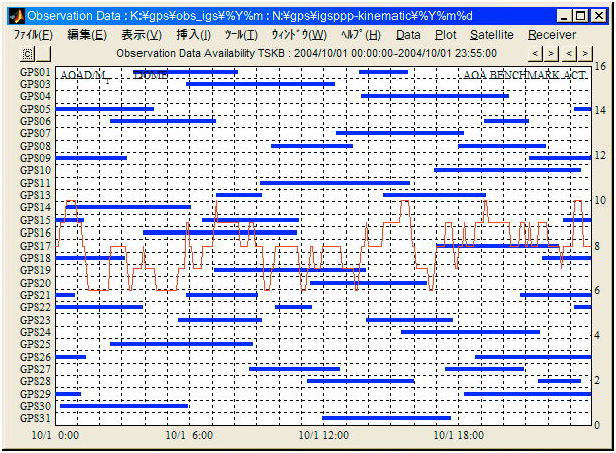
観測データには同時観測した複数衛星の測位信号測定値が含まれる。現在運用中の GPS衛星は30衛星であり位置に依存するが常時4〜10機のGPS衛星からの測位信号を受信できるのが普通である。衛星毎観測期間と観測衛星数の推移の例を図A.4.12に示す。この観測点の例では常時6〜10衛星の観測データが得られている。
図
A.4.12 衛星毎観測期間と観測衛星数の推移例
精密解析で使用する観測データには擬似距離及び搬送波位相測定値が含まれる。二周波解析の場合は L1、L2擬似距離及び搬送波位相測定値が含まれる観測データを使用する。なお観測データにはL1擬似距離測定値としてC/AコードによるC1とPコードによるP1の両者が含まれる場合がある。二周波受信機で観測したL1、L2擬似距離測定値の例を図A.4.13に搬送波位相測定値の例を図A.4.14に示す。
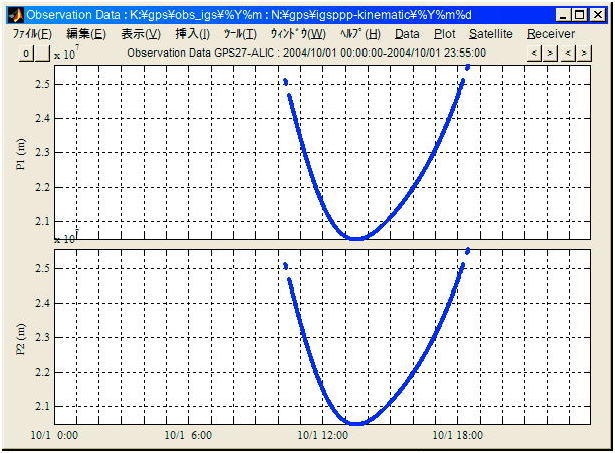
図 A.4.13 L1,L2擬似距離測定値の例
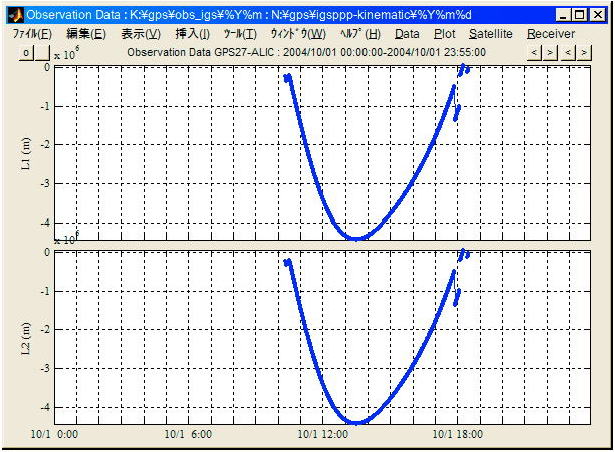
図 A.4.14 L1,L2搬送波位相測定値の例
図A.4.14の搬送波位相測定値の端の方で測定値が乱れ、飛んでいるのがいわゆるサイクルスリップである。この例では大きな飛びが発生しているため識別可能だがより小さいサイクルスリップでは搬送波位相測定値をプロットして見ても殆ど識別できないことが多い。
RINEX観測データの分割、併合、ヘッダ情報修正等の編集が必要になることがある。この目的のツールの中で最も一般的なユーティリティがUNAVCO(University NAVSTAR Consortium)で開発されたTEQCである。TEQCは受信機独自データ形式とRINEX形式間の変換機能、RINEX観測データの編集機能を持つ他に、QCモードと呼ぶ品質チェック機能が付加されている。TEQCのQCモードではRINEX観測データ、航法メッセージデータを入力すると観測データ数、マルチパス、サイクルスリップ数等の統計情報をレポートとして出力してくれるのでそれにより観測データの品質をチェックすることができる。図A.4.15にTEQCのQCモードレポート出力結果例を示す。
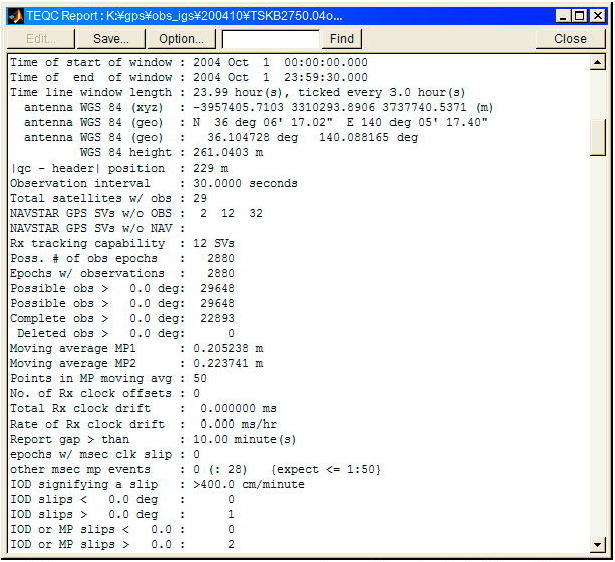
図
A.4.15 TEQC QCモードレポート出力例(一部)
観測データの前処理段階で後の解析処理で使用するため、放送暦及び擬似距離測定値を使用した単独測位により観測時刻毎に衛星位置、観測点位置、受信機時計誤差、衛星方位・仰角等の概略推定値が求めることが多い。ここで単独測位については適当な文献を参照のこと。単独測位で求めた衛星位置、観測点位置、受信機時計誤差等の概略推定値は後の解析処理で以下の目的に使用される。
(1)
受信機時計飛びの検出
(2)
サイクルスリップ検出
(3)
観測点位置推定初期値
(4)
受信機時計誤差推定初期値
(5)
幾何学距離算出時の受信機時計誤差項
(6)
仰角カットオフ判定
(7)
衛星の食期間判定
(8)
異常衛星検出・除外
GPS/GNSS受信機の中には受信機時計誤差が一定値以上大きくならないよう周期的に受信機時計の飛びを起こして時計を修正するものがある。この受信機時計の動作はClock Steeringと呼ばれる。これらの受信機では時計飛びと同時に擬似距離測定値に飛びが発生する場合がある。受信機時計飛びを起こしている受信機の擬似距離測定値の例を図A.4.16に示す。擬似距離測定値の飛びは後から述べるサイクルスリップ検出において誤動作を引き起こすため、観測データ前処理の段階でこれらの飛びを検出して観測データを修正することが行われる。
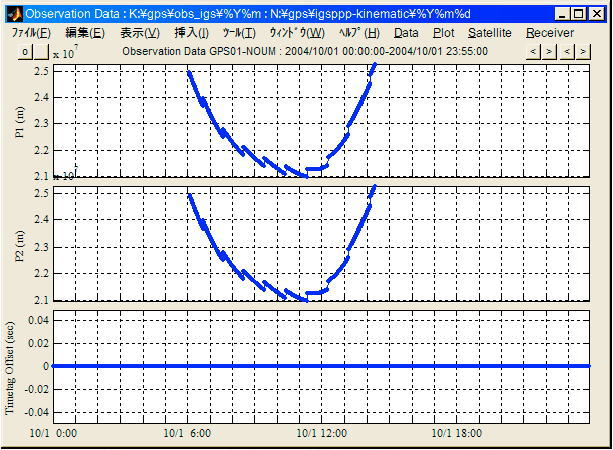
図
A.4.16 擬似距離測定値飛びの例
擬似距離測定値飛びの検出には直接擬似距離測定値の観測時刻間差により検出する方法や単独測位による受信機時計誤差推定値の飛びを検出する方法が取られる。検出された擬似距離測定値飛びは以下の様に修正する。観測時刻を![]() としその時の擬似距離測定値を
としその時の擬似距離測定値を![]() とする。受信機時計飛び位置を
とする。受信機時計飛び位置を![]() 、時計飛び量を
、時計飛び量を![]() (sec)として修正後の観測時刻
(sec)として修正後の観測時刻![]() 、擬似距離測定値
、擬似距離測定値![]() は以下の様に示される。ここで時計飛び量
は以下の様に示される。ここで時計飛び量![]() は時計飛び推定値を1 msecの倍数に丸めた値が用いられる。
は時計飛び推定値を1 msecの倍数に丸めた値が用いられる。
![]()
(![]()
以上のように受信機時計飛び以降の擬似距離測定値から一定の時計オフセット分を引いて測定値の飛びを解消すると同時に観測時刻をそれと矛盾しないように修正する。擬似距離![]() は(A.4.1)に示すように観測時刻から衛星送信時刻を引いて光速を掛けたものと定義されるので以上の修正で解析に使う観測モデルを変更する必要はない。なおここで通常搬送波位相測定値に飛びは発生しないので修正しない。受信機時計飛び修正後の擬似距離測定値の例を図A.4.17に示す。図の下段は修正後観測時刻の修正前観測時刻との差分を示している。
は(A.4.1)に示すように観測時刻から衛星送信時刻を引いて光速を掛けたものと定義されるので以上の修正で解析に使う観測モデルを変更する必要はない。なおここで通常搬送波位相測定値に飛びは発生しないので修正しない。受信機時計飛び修正後の擬似距離測定値の例を図A.4.17に示す。図の下段は修正後観測時刻の修正前観測時刻との差分を示している。
以上の擬似距離測定飛びの修正は精密解析の前に、受信機または RINEX観測データ出力時に行われている場合が有る。その場合でも複数観測データを併合して長時間の解析を行う場合、その観測データ間の繋ぎ目で同様の擬似距離測定値飛びが現れることがありその場合は同様に修正を行う必要がある。
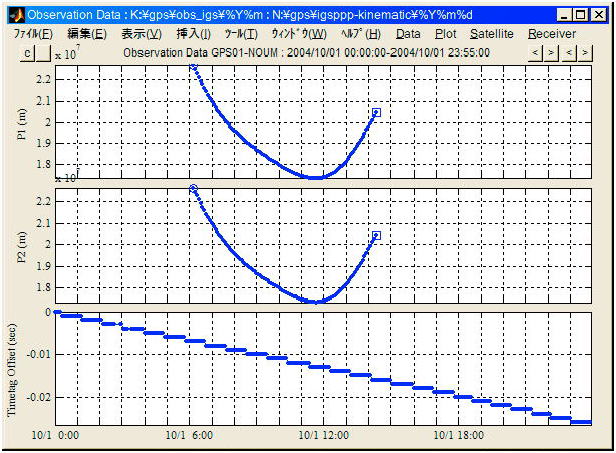
図
A.4.17 受信機時計飛び修正後の擬似距離測定値
搬送波位相測定値を使った精密測位においてサイクルスリップの検出及び修正は重要な課題であり信頼性の高いサイクルスリップ検出及び修正は測位精度の向上に欠かせないものである。なおサイクルスリップ検出及び修正を後のパラメータ推定時に同時に行う場合もあるが一般には観測データ前処理の段階で行うことが多い。
サイクルスリップは搬送波位相バイアスの整数不定性が別の値に設定される現象なので搬送波位相測定値の飛びとして現れる。ただし測定値には幾何学距離、時計誤差等の大きな時間変動が乗っているため直接はそれらの変動とサイクルスリップとを区別するのが難しい。従って複数観測量の線形結合により搬送波位相測定値の飛びを強調し検出することが行われる。搬送波位相測定値の観測時刻間の二重差、三重差を使って飛びを検出する場合も有る。相対測位の場合はこれらの検出は観測量の二重差を取った後に行われることが多い。これは時計誤差項、対流圏遅延、電離層遅延項が消去または低減されるためサイクルスリップを検出し易くなることによる。
さてサイクルスリップ検出には以上のように各種の手法があるが測定値の差を取らないサイクルスリップ検出方法として一般的な手法である二周波搬送波位相と擬似距離測定値を併用して検出する方法を例として以下に紹介する。この手法では幾何学フリー線形結合および
Melbourne-Wübbena線形結合を使用してサイクルスリップを検出しそのスリップ量を推定する。搬送波位相幾何学フリー線形結合![]() の定義と観測モデルを再掲すると以下の様になる。
の定義と観測モデルを再掲すると以下の様になる。
![]()
![]() には幾何学項が消えて電離層遅延項と搬送波位相バイアス項のみ残っており観測誤差
には幾何学項が消えて電離層遅延項と搬送波位相バイアス項のみ残っており観測誤差![]() も通常は
cm以下の値である。サイクルスリップ時には搬送波位相バイアス
も通常は
cm以下の値である。サイクルスリップ時には搬送波位相バイアス![]() に整数値の飛びが表れるがこの際に
に整数値の飛びが表れるがこの際に![]() に現れる飛びを表A.4.6に示す。
に現れる飛びを表A.4.6に示す。
| L1/L2 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | -24 | -49 | -73 | -98 | -122 | -147 | -171 | -195 | -220 | -244 |
| 1 | 19 | -5.4 | -10 | -54 | -79 | -103 | -128 | -152 | -176 | -201 | -225 |
| 2 | 38 | 14 | -11 | -35 | -60 | -84 | -109 | -133 | -157 | -182 | -206 |
| 3 | 57 | 33 | 8.2 | -16 | -41 | -65 | -89 | -114 | -138 | -163 | -187 |
| 4 | 76 | 52 | 27 | 2.9 | -22 | -46 | -70 | -95 | -119 | -144 | -168 |
| 5 | 95 | 71 | 46 | 22 | -2.5 | -27 | -51 | -76 | -100 | -125 | -149 |
| 6 | 114 | 90 | 65 | 41 | 17 | -7.9 | -32 | -57 | -81 | -106 | -130 |
| 7 | 133 | 109 | 84 | 60 | 36 | 11 | -13 | -38 | -62 | -87 | -111 |
| 8 | 152 | 128 | 103 | 79 | 55 | 30 | 5.7 | -19 | -43 | -68 | -92 |
| 9 | 171 | 147 | 122 | 98 | 74 | 49 | 25 | 0.3 | -24 | -49 | -73 |
| 10 | 190 | 166 | 142 | 117 | 93 | 68 | 44 | 19 | -5.1 | -30 | -54 |
搬送波位相バイアス![]() の飛び量をそれぞれ
の飛び量をそれぞれ![]() としてサイクルスリップを
としてサイクルスリップを![]() で表すと(9,7)以外のスリップは
で表すと(9,7)以外のスリップは![]() に大きさで2.5 cm以上の飛びとして現れる。従って電離層遅延
に大きさで2.5 cm以上の飛びとして現れる。従って電離層遅延![]() の時間変動がこの値に比較し十分小さければ
の時間変動がこの値に比較し十分小さければ![]() の観測時刻間差を適当な閾値と比較することによりサイクルスリップを検出することができる。すなわち観測時刻
の観測時刻間差を適当な閾値と比較することによりサイクルスリップを検出することができる。すなわち観測時刻![]() の搬送波位相幾何学フリー線形結合を
の搬送波位相幾何学フリー線形結合を![]() (m)、最大L1電離層遅延変動を
(m)、最大L1電離層遅延変動を![]() (m/sec)として以下を満たす
(m/sec)として以下を満たす![]() をスリップ位置と判定する。
をスリップ位置と判定する。
![]()
以上の搬送波位相幾何学フリー線形結合では検出困難なサイクルスリップ例えば(9,7)は他の線形結合を使って検出する。Melbourne-Wübbena線形結合![]() の定義と観測モデルを以下に再掲する。
の定義と観測モデルを以下に再掲する。
![]()
![]() にはサイクルスリップが発生しなければ定数となる搬送波位相バイアス項と観測誤差項のみを含む。またワイドレーン波長
にはサイクルスリップが発生しなければ定数となる搬送波位相バイアス項と観測誤差項のみを含む。またワイドレーン波長![]() でありサイクルスリップ時には大部分のケースで
86 cm以上の飛びを生じる。例えば(9,7)のスリップでは172
cmの飛びが現れるので観測時刻間の差を取ることによりサイクルスリップを検出することが出来る。ただし低仰角の擬似距離測定値にはしばしばマルチパスの影響による1mを超える観測誤差が乗り大きく変動するためこれらの雑音成分による誤検出を避けるため平滑化を行う。よく使われるのは移動平均フィルタでスリップ判定点の前後ぞれぞれの何点かの測定値の平均をとって比較し飛びを検出する。すなわち観測時刻
でありサイクルスリップ時には大部分のケースで
86 cm以上の飛びを生じる。例えば(9,7)のスリップでは172
cmの飛びが現れるので観測時刻間の差を取ることによりサイクルスリップを検出することが出来る。ただし低仰角の擬似距離測定値にはしばしばマルチパスの影響による1mを超える観測誤差が乗り大きく変動するためこれらの雑音成分による誤検出を避けるため平滑化を行う。よく使われるのは移動平均フィルタでスリップ判定点の前後ぞれぞれの何点かの測定値の平均をとって比較し飛びを検出する。すなわち観測時刻![]() のMelbourne-Wübbena線形結合を
のMelbourne-Wübbena線形結合を![]() (m)、平均化観測点数を
(m)、平均化観測点数を![]() 、スリップ検出閾値を
、スリップ検出閾値を![]() (m)として以下を満たす
(m)として以下を満たす![]() をスリップ点と判定する。
をスリップ点と判定する。
![]()
ただしこの方法では L1、L2搬送波位相が同一量スリップした場合、例えば(1,1)、(2,2)等のサイクルスリップは検出できない。また以上の方法ではL1、L2搬送波位相のどちらがサイクルスリップを起こしているか、あるいは両者がスリップしているか判断ができないことに注意のこと。
搬送波位相測定値に発生したサイクルスリップが線形結合![]() に現れた例を図
A.4.18に示す。この例では観測時刻19:11にサイクルスリップが発生し
に現れた例を図
A.4.18に示す。この例では観測時刻19:11にサイクルスリップが発生し![]() が約20cm、
が約20cm、![]() が1cycle(86cm)の飛びを起こしている。表A.4.6からこれは(1,0)のサイクルスリップであることが分かる。実際の観測データではこの例の様な小さいサイクルスリップは少なくずっと大きな飛びを示すことが多いのでその場合サイクルスリップの検出はもっと容易である。
が1cycle(86cm)の飛びを起こしている。表A.4.6からこれは(1,0)のサイクルスリップであることが分かる。実際の観測データではこの例の様な小さいサイクルスリップは少なくずっと大きな飛びを示すことが多いのでその場合サイクルスリップの検出はもっと容易である。
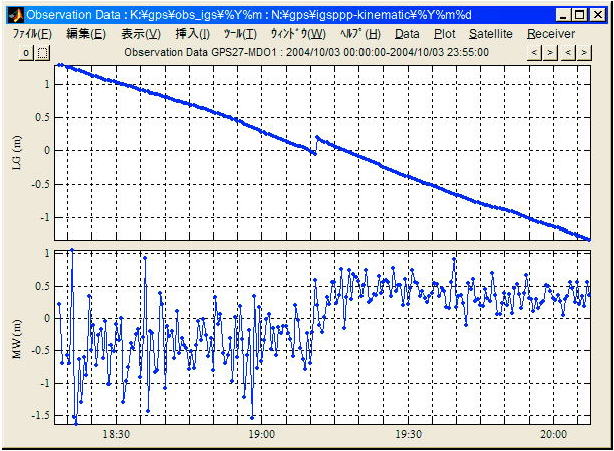
図 A.4.18 ![]() に現れたサイクルスリップの例
に現れたサイクルスリップの例
以上がサイクルスリップ検出の基本的な原理であるが現実の観測データでは単純には行かない。まず![]() 飛びの検出では電離層遅延の時間変動が十分に小さいことを仮定していたが太陽活動活発期や低緯度観測点ではよく電離層遅延の大きな時間変動を起こすため差を取らない測定値ではサイクルスリップとの識別が難しい場合が多い。特に観測時刻間隔が
30secの様に長い場合、大きな電離層遅延変動をサイクルスリップと誤判定してしまうのを完全に避けるのは困難である。
飛びの検出では電離層遅延の時間変動が十分に小さいことを仮定していたが太陽活動活発期や低緯度観測点ではよく電離層遅延の大きな時間変動を起こすため差を取らない測定値ではサイクルスリップとの識別が難しい場合が多い。特に観測時刻間隔が
30secの様に長い場合、大きな電離層遅延変動をサイクルスリップと誤判定してしまうのを完全に避けるのは困難である。![]() 飛びによる検出も擬似距離測定値に含まれるマルチパスが大きい場合には誤検出や検出漏れを起こしやすい。これらの検出漏れを防ぐため、その他の線形結合例えばL1、L2マルチパス線形結合
飛びによる検出も擬似距離測定値に含まれるマルチパスが大きい場合には誤検出や検出漏れを起こしやすい。これらの検出漏れを防ぐため、その他の線形結合例えばL1、L2マルチパス線形結合![]() 等を組み合わせて検出に使用する場合もある。
等を組み合わせて検出に使用する場合もある。
次にサイクルスリップ修正の手法につき説明する。サイクルスリップ修正にはまず
L1、L2搬送波位相それぞれのスリップ量を推定する必要がある。最初に電離層遅延の時間変動が短い時間内では十分に滑らかであると仮定して多項式Fittingにより搬送波位相幾何学フリー線形結合のスリップ量を推定する。上記手順で求めたサイクルスリップ検出点を![]() 、スリップ量推定に使用するスリップ点前後観測点数を
、スリップ量推定に使用するスリップ点前後観測点数を![]() 、Fittingに使用する多項式の次数を
、Fittingに使用する多項式の次数を![]() として搬送波位相幾何学フリー線形結合スリップ量
として搬送波位相幾何学フリー線形結合スリップ量![]() (m)は以下で求められる。
(m)は以下で求められる。
![]()
![]()
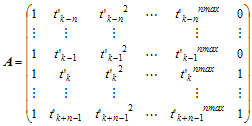
![]()
次にワイドレーンスリップ量を推定する。スリップ量推定に使用するスリップ点前後観測点数を![]() としてワイドレーンスリップ量
としてワイドレーンスリップ量![]() (m)は以下で求められる。
(m)は以下で求められる。
![]()
L1
、L2搬送波位相スリップ量を![]() (cycle)として以下の連立方程式を解いて解を適当な整数に丸めることにより各スリップ量を求めることができる。
(cycle)として以下の連立方程式を解いて解を適当な整数に丸めることにより各スリップ量を求めることができる。
![]()
以上で
L1、L2搬送波位相毎のスリップ量が求まる。観測時刻![]()
![]() のサイクルスリップ修正後のL1、L2搬送波位相測定値を
のサイクルスリップ修正後のL1、L2搬送波位相測定値を![]() (m)として以下の様にサイクルスリップ修正を行うことができる。
(m)として以下の様にサイクルスリップ修正を行うことができる。
![]()
![]()
サイクルスリップ修正の原理は以上であるが現実の観測データではしばしばスリップ量推定が難しい場合がある。まず上記連立方程式を解いて解を整数に丸める際に信頼度よく丸めることが出来ない場合がある。これは電離層遅延時間変動や擬似距離測定値に載ったマルチパスにより各線形結合のスリップ量推定値の精度が良くないことが主な原因である。またサイクルスリップが連続的に発生したり前後の測定値が欠落することがよくあり、この際もスリップ量推定値の誤差が大きくなる。従って信頼度良くスリップ量を確定できない場合には修正はあきらめスリップ位置のみ記録し前後の観測データを別々のアークと見なして別々の搬送波位相バイアスを推定することになる。サイクルスリップの誤修正は測位精度を非常に悪化させるのでスリップ量推定値の信頼度が低い場合は修正を行わないほうが結果が良くなることが多い。
サイクルスリップ修正の必要性はスタティック測位とキネマティック測位とではずいぶん異なる。スタティック測位ではもともとサイクルスリップ頻度が少ないし実際修正を行っても精度改善は僅かである。従って一般的には誤修正のリスクを負ってまで修正を行うメリットはあまりない。これに比較しキネマティック測位では頻繁にサイクルスリップが起きる場合が多いし、修正を行わない場合、再初期化が必要になったり測位精度が大きく悪化する場合が多い。従ってサイクルスリップ修正を行うか否かは状況を良く見て判断する必要がある。
以上で観測データの前処理が終わり、サイクルスリップが検出・修正された搬送波位相測定値が得られる。後はこれらの観測データを使ってA.4.4、A.4.5で説明した精密測位の手法に従って観測点位置等を未知パラメータとして推定を行うことになる。
ここで特にスタティック測位においては推定に使用する観測データの間引きを行うことが多い。これは例えば 30秒間隔の観測データから5分間隔の測定値のみを抽出し、推定にはそのデータのみ使用するといった操作である。この目的は主に解析時間の削減であるが高時間分解能の観測データが必ずしも高精度に結びつかないという理由もある。これは観測時刻の近い観測データにはマルチパスや対流圏遅延補正残差等相関の高い系統誤差が含まれることが多く各測定値間の独立性が必ずしも良くないためであると考えられる。
観測データ中には異常な値を示すデータが含まれることがありこれが精密解析における推定値精度を劣化させる。異常データの原因は様々だが単なる観測誤差以外に、例えば機器の故障、データ転送エラー、プログラムバグ、人為的なミス等が含まれる。
A.4.2.3で示した衛星の予期しない動作や不調が原因の場合も有る。これらの異常観測データは時に1000mを超える誤差を示すためこれらのデータを識別し除外しないと推定値に大きな誤差を引き起こすことになる。これらの異常観測データはアウトライア(Outlier)と呼ばれる。これらの異常データを識別するためには事後残差(postfit
residuals)の検査を行う。観測データを![]() 、観測モデルを
、観測モデルを![]() 、最小二乗法で求まった未知パラメータの推定値を
、最小二乗法で求まった未知パラメータの推定値を![]() として事後残差
として事後残差![]() は以下の様に表せる。
は以下の様に表せる。
![]()
ここで事後残差を![]() 、観測誤差標準偏差をを
、観測誤差標準偏差をを![]() として以下を満たす観測データ
として以下を満たす観測データ![]() をアウトライアとして識別する。
をアウトライアとして識別する。
![]()
ここで通常![]() は
4〜5とする。識別されたアウトライアは観測データから除去され、残りの観測データを使って再度パラメータ推定を行い最終的にアウトライアが検出されなくなるまで繰り返す。カルマンフィルタではアウトライアに対してより敏感で異常観測データが原因で解析途中で推定値が発散することがあるためより厳格にこれらのチェックを行う必要がある。
は
4〜5とする。識別されたアウトライアは観測データから除去され、残りの観測データを使って再度パラメータ推定を行い最終的にアウトライアが検出されなくなるまで繰り返す。カルマンフィルタではアウトライアに対してより敏感で異常観測データが原因で解析途中で推定値が発散することがあるためより厳格にこれらのチェックを行う必要がある。
その他、衛星毎、観測点毎のアウトライア率や事後残差 RMS等の統計情報を使って異常衛星や異常観測点を識別し衛星、観測点ごと観測データの除去を行うこともある。
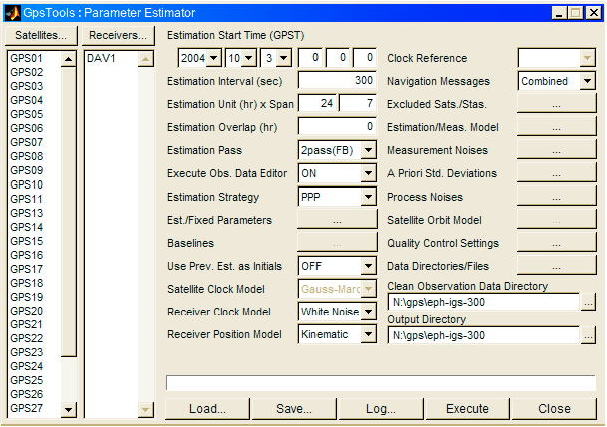
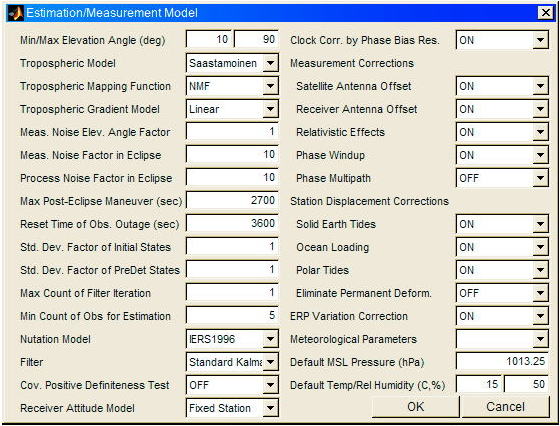
さて以上で示した精密解析を行うには通常 GPS/GNSS用精密解析ソフトウェアを使用する。ここでこれらのソフトウェアを使用した解析の例として筆者が開発中の精密解析ソフトウェアGpsTools(GT)を使って地上観測点の精密測位を行った例を示す。使用した観測データを図A.4.19に示す。また解析パラメータ設定値を図A.4.20に示す。上段が全体の解析条件設定画面であり、使用衛星、観測点、推定開始日時、推定間隔、推定期間、推定パス、推定戦略、推定・固定パラメータ、推定モデル、入出力ディレクトリ等を設定している。下段が推定・観測モデルの詳細パラメータ設定でありカットオフ角、対流圏遅延モデル、対流圏マッピング関数、観測誤差パラメータ、使用フィルタ、精密観測補正項のOn/Off、局位置変動モデルのOn/Off、気象パラメータ等を設定している。その他観測誤差、初期値標準偏差、プロセスノイズ標準偏差、品質管理パラメータ、各種設定ファイル等を設定する必要がある。

図
A.4.19 使用観測データ
図
A.4.20 解析パラメータの設定
この例ではキネマティック PPPにより24H 300sec間隔で観測点位置を推定している。以上の解析で得られた観測点位置推定値のプロットを図A.4.21に示す。ここで左が水平方向、右が垂直方向のばらつきを示している。この例では南北方向2cm以内、東西方向1cm以内、上下方向4cm以内程度の位置再現性が得られている。
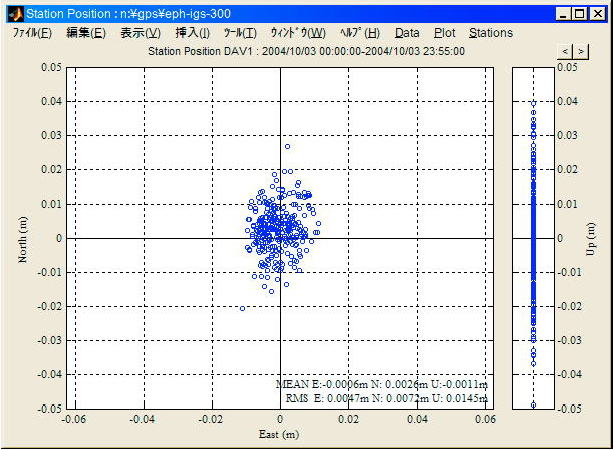
図 A.4.21 測位結果の表示
以上の解析時に出力された解析ログファイルを図A.4.22に示す。解析ソフトウェアにもよるが解析時の推定条件、統計情報、残差、警告や情報を解析ログファイルとして同時出力する場合が多い。
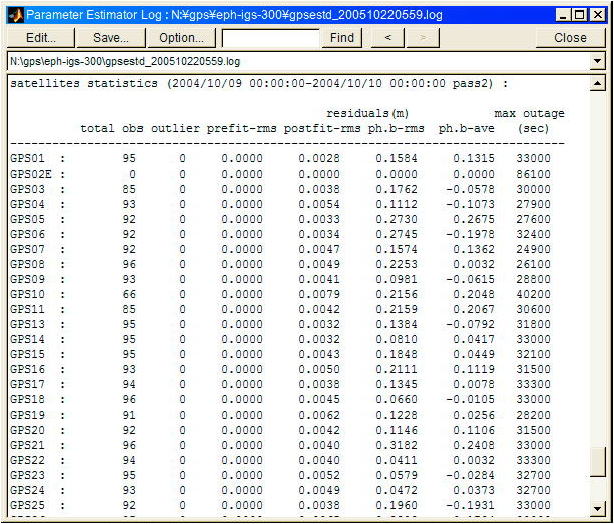
図
A.4.22 解析ログファイル(一部)
| A.4.5 精密単独測位(PPP)← | →A.4.7 おわりに |
| Copyright (C) 2005 by Tomoji Takasu, All rights reserved |