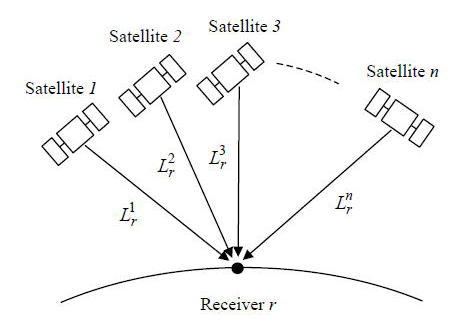
図 A.4.10 精密単独測位の概念図
|
搬送波位相測定値による精密測位の理論及び解析処理 |
Home |
A.4.5 精密単独測位(PPP)
A.4.5.1 精密単独測位の手法
A.4.5.2 精密単独測位の応用
精密単独測位 (PPP : Precise Point Positioning) /9/ は単独観測点のみで測位を行う精密測位法であり相対測位と異なり基準観測点を必要としない。以下に精密単独測位の原理と手法につき説明する。
精密単独測位の原理は擬似距離を使った通常の単独測位と同様であり、衛星軌道・時計を既知として固定し複数衛星の測位信号観測値を使って観測点位置と受信機時計誤差を推定する。ただし精密単独測位では基本観測量として差をとらない (Undifferenced)搬送波位相を使用するためより高精度の測位が可能となる。単独測位と精密単独測位の比較を表A.4.4に示す。
| 項目 | 単独測位 | 精密単独測位 |
|---|---|---|
| 基本観測量 | 擬似距離 | 搬送波位相 |
| 軌道・時計 | 放送暦 | 精密暦 |
| 電離層遅延 | モデル補正 | 二周波線形結合 |
| 対流圏遅延 | モデル補正 | モデル+推定 |
| 位相バイアス | なし | 推定 (Float) |
| 精密補正 | なし | 有り |
以下に、精密単独測位についてカルマンフィルタを使って推定を行う例を使ってその手法を説明する。

図
A.4.10 精密単独測位の概念図
地球固定座標系での観測点![]() の位置を
の位置を![]() とする。観測点
とする。観測点![]() で一定期間衛星
で一定期間衛星![]() の二周波搬送波位相測定を行いその観測データが得られたとする。また観測期間中にサイクルスリップは発生しないと仮定する。以上の前提でカルマンフィルタで推定する未知パラメータ
の二周波搬送波位相測定を行いその観測データが得られたとする。また観測期間中にサイクルスリップは発生しないと仮定する。以上の前提でカルマンフィルタで推定する未知パラメータ![]() を以下と置く。
を以下と置く。
![]()
ここで観測点位置![]() 以外に受信機時計誤差
以外に受信機時計誤差![]() 、観測点の天頂湿潤遅延
、観測点の天頂湿潤遅延![]() 、電離層フリー線形結合搬送波位相バイアス
、電離層フリー線形結合搬送波位相バイアス![]() を未知パラメータとしている。
を未知パラメータとしている。
観測開始時の![]() の概略推定値を
の概略推定値を![]() 、その推定誤差標準偏差を
、その推定誤差標準偏差を![]() として、カルマンフィルタにおける初期推定値
として、カルマンフィルタにおける初期推定値![]() 及び初期推定値共分散行列
及び初期推定値共分散行列![]() を以下の様に置く。なおここで観測開始時の概略推定値は単独測位、標準大気モデル、擬似距離測定値等から求める。
を以下の様に置く。なおここで観測開始時の概略推定値は単独測位、標準大気モデル、擬似距離測定値等から求める。
![]()
![]()
観測期間中の観測時刻を![]() とする。観測時刻
とする。観測時刻![]() で得られた搬送波位相測定値を使って以下の観測量ベクトルを作る。ここで
で得られた搬送波位相測定値を使って以下の観測量ベクトルを作る。ここで![]() は衛星
は衛星![]() の搬送波位相電離層フリー線形結合を示す。
の搬送波位相電離層フリー線形結合を示す。
![]()
以上より、観測モデル、計画行列及び観測誤差共分散行列は(A.4.8)を使って以下で表される。
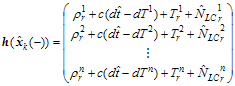
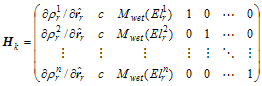
![]()
ここで![]() は時刻
は時刻![]() の観測点位置の更新前推定値
の観測点位置の更新前推定値![]() を使って求めた幾何学距離である。
を使って求めた幾何学距離である。![]() は衛星
は衛星![]() の衛星時計誤差で精密暦から求める。
の衛星時計誤差で精密暦から求める。![]() は対流圏遅延であり天頂湿潤遅延推定値
は対流圏遅延であり天頂湿潤遅延推定値![]() を使った対流圏遅延モデルから求める。また
を使った対流圏遅延モデルから求める。また![]() は湿潤遅延マッピング関数、
は湿潤遅延マッピング関数、![]() は衛星仰角、
は衛星仰角、![]() は観測
は観測![]() の観測誤差標準偏差である。以上をカルマンフィルタの観測更新則(A.4.19)に適用することにより時刻
の観測誤差標準偏差である。以上をカルマンフィルタの観測更新則(A.4.19)に適用することにより時刻![]() における未知パラメータ推定値
における未知パラメータ推定値![]() 及び推定値共分散行列
及び推定値共分散行列![]() が得られる。
が得られる。
受信機時計の時間変動はWhite-Noiseモデル、天頂湿潤遅延の時間変動はRandom-Walk過程でモデル化するものとし、観測点位置は一定すなわちスタティック測位の場合とするとカルマンフィルタの時間更新則は以下の様に書ける。
![]()
![]()
![]()
![]()
ここで![]() はそれぞれ
はそれぞれ![]() における観測更新前推定値、
における観測更新前推定値、![]() は単独測位等で求めた受信機時計誤差概略推定値、
は単独測位等で求めた受信機時計誤差概略推定値、![]() は
は![]() の推定誤差標準偏差、
の推定誤差標準偏差、![]() は天頂湿潤遅延のプロセスノイズ標準偏差、
は天頂湿潤遅延のプロセスノイズ標準偏差、![]() である。キネマティック測位の場合には上記の時間更新則を以下に様に変更する。
である。キネマティック測位の場合には上記の時間更新則を以下に様に変更する。
![]()
![]()
![]()
![]()
ここで![]() は単独測位等で求めた観測点
は単独測位等で求めた観測点![]() の位置概略推定値、
の位置概略推定値、![]() は
は![]() の
の![]() 成分推定誤差標準偏差である。後は逐次上記の手順を繰り返すことにより観測時刻
成分推定誤差標準偏差である。後は逐次上記の手順を繰り返すことにより観測時刻![]() での未知パラメータ推定値
での未知パラメータ推定値![]() が得られる。
が得られる。
以上が単純化したカルマンフィルタによる精密単独測位の手法であるが相対測位と同様に実際の解析においては色々な考慮が必要になる。
カルマンフィルタでは未知パラメータの時間変動モデルや他の測定値を推定プロセスに導入するのが容易だというメリットがあり、例えばキネマティック測位に適用した場合、観測点特有の運動モデルを時間更新則に追加したりINS等他のセンサの測定値を導入したりすることによりより精密な位置推定や運動モデルパラメータ推定等が可能となる。
なお、以上の例ではカルマンフィルタを用いた精密単独測位の手法を説明したが最小二乗法を使っても同様の推定が可能である。
精密単独測位では、相対測位と異なり二重差による各種誤差要因が消去または低減されないため精密な補正が必須となる。従って、上記でも電離層遅延に関しては電離層フリー線形結合、対流圏遅延については推定パラメータを使った精密モデルで補正を行っている。それ以外の受信アンテナ位相中心、局位置変動、Phase-Windup等の誤差要因についても、必要な精度に応じて先に説明したモデルを使って補正を行う必要がある。
精密単独測位の応用として重要な技術について以下に簡単に紹介する。
(1) キネマティックPPP
相対測位と同様に、精密単独測位でも移動体の精密測位が可能で有りキネマティック PPPと呼ばれる。航空機等の高速移動体の場合、相対測位では基準観測点を順次切り替える等の操作が必要になり解析が複雑になるが、精密単独測位では基準観測点が不要で解析が容易である。GPS受信機を搭載した低軌道衛星の精密軌道決定に使われることもある。
(2) GDGPS(Global Differential GPS)
リアルタイムで決定した GPS/GNSS衛星の精密軌道・時計情報を、通信衛星等を使ってユーザに送信することにより精密単独測位によりユーザの精密位置決定を行う技術である。通常のDGPSと異なり全世界でサービスが利用可能であり搬送波位相を使うためより精度が高い。既にいくつかの商用サービスが開始されている。
(3) 精密時刻同期
相対測位では二重差により時計誤差を消去して推定を行うため受信機時計の推定が直接はできない。これに比べ精密単独測位では観測点の受信機時計誤差を高精度に推定することができ、良い条件のもとで 100 psec程度の精度が得られると言われている。地上の複数基準時計間の精密時刻同期に精密単独測位が利用されている。
(4) 可降水量分布推定
精密単独測位では測位と同時に対流圏遅延パラメータの推定が可能であり天頂湿潤遅延からは観測点の鉛直総水蒸気量である可降水量が推定できる。多数観測点の観測データを使って精密単独測位により可降水量の分布を求めることが行われている。特に精密単独測位は相対測位に比較し多数観測点解析の際の計算量が少ない等のメリットがある。
| A.4.4 相対測位← | →A.4.6 精密解析の実際 |
| Copyright (C) 2005 by Tomoji Takasu, All rights reserved |