|
日記・備考録 |
2005 | 2006/1 2 3 4 5 6 7 8 9 10 11 12 | 2007 |
| February | March 2006 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
April | Home |
.....................................................................................................................................
Proceedings of 15th Workshop on JAXA Astrodynamics
and Flight Mechanics, Jul 25 - Jul 26, 2005, ISAS/JAXA
2005アストロダイナミクスシンポジウム後刷り論文集がJAXAから届く。GPS高精度軌道決定掲載。再度読み返すと稚拙な英語。もう少しなんとかしないといけない。まあ内容はそれなりのレベルだとは思うが。添付案内にはISAS/JAXAのWebサイトからオンライン閲覧可能と書かれているが今日時点ではまだ更新されていない様だ。2006年は7/31-8/1に開催予定らしい。
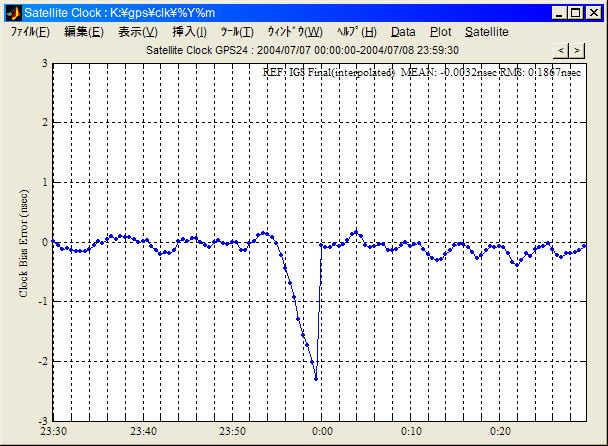
ニューリアルGTでGRACE衛星POD。純Kinematic。アーク単位QCやcycle-slip検出等色々改良し無駄な部分を省いて高速した。GRACE 2衛星の30s-PPP1ヶ月分で約50分。地上局20局 30s-PPP 24Hで約5分。随分と速くなった。ただLEO衛星PODの長期評価で7cm(3D)を切るのはなかなか難しい。どうしてもスパイク状誤差がたまに出る。300s時計と30s時計の差を発表したいのだが実際やってみると思ったほど改善されるわけではない。これではあまり面白くない。
とりあえずGRACE-A 30sキネマティックPPP 2ヶ月分の結果を貼っておく。JPL60s解比較。IGS-COD-30s時計。CODE時計は簡単なQCによるスクリーニング。アーク単位の残差RMS/アウトライア率による除外/再推定を入れた。運動モデルを入れないとこれ以上の精度は難しそう。なおJPL解とはradial方向2-3cmのバイアスが出ているのでこれを補正するともう少し差が小さくなる。

昨日LEO衛星PODでは運動モデル精度10-5m/s2あれば十分と書いた。これに比較しGPS衛星PODの場合10-10m/s2は欲しいと以前書いた。この差は何か。どちらも搬送波位相を使うからちょっと考えると同じ様な気もするが実際は大きく違う。これは主にgeometryの違いに起因する。GPS衛星の場合観測局は地上にしかないから観測視線方向の広がりが狭くなり所謂DOP値が非常に大きくなり運動モデルによる補完が必須になる。また運動モデルが良くないと観測値から軌道と時計をうまく分離できない。それに比較しLEO衛星ではDOP条件が遥かに良くなり運動モデルなしでも条件が良ければ十分な精度が出る。運動モデルは条件が悪い時間帯を補完するためだけに必要となる。
.....................................................................................................................................
JGM-3 Geopotential Model
JGM-3重力ポテンシャル係数。現在GTにはGPS衛星POD用に12次までのJGM-3係数が入っているがLEO衛星用に次数を上げるため。IERS
Conventions 1996ではJGM-3が推奨モデルだったが2003ではEGM96に変更されているので今使うならEGM96の方が良いかもしれない。ただJGM-3とEGM96ではC20の永年潮汐補正項の扱いが異なる(zero-frequency-tide
or tide-free)ので注意する必要がある。高度500kmの衛星なら30次くらいまでは入れたほうが良いのだろうか。あとはAir
Dragを入れる予定だが大気密度のモデルは何を使うのが良いのかよく分からない。Montenbruck
3.5に各種モデルの比較があり参考になるが、どうせGPS搭載衛星では十分密で精度の良い観測データが存在するので運動モデルはあまり効かないはず。10-5m/s2程度の精度が出れば十分だろう。
.....................................................................................................................................
MATLAB Programing, The Mathworks
matlabプログラミングチュートリアル。matlabにはオンラインマニュアルに載っていない
(もしかすると載っているかもしれないが簡単には見つからない)
プログラム言語featureが多い。例えば以下の様なもの。使いこなすとプログラムがコンパクトに書ける。今考えると信じられないが使い出しの頃は(マニュアル通り)スカラーで割るのに一々./とドットをつけていた。
(1) x=x(find(~x)) -> x=x(~x);
(2) x=reshape(y,n,1), y=reshape(x,n,m); ->
x=y(:); y(:)=x;
(3) [a{1},a{2},...] -> [a{:}]
(4) privateフォルダによる関数隠蔽
.....................................................................................................................................
GTのリストラ。機能追加しすぎで構造がぐちゃぐちゃなのをシンプルに。次に二度と使わない機能を削除し解析エンジン部を約50%にスリム化。一通り動くようになったらちょっとだけ機能追加して、単体試験ルーチンをちゃんと書いて正式版(ver.1.0)化予定。精度には殆ど効かない細かいバグをいくつか発見。よくこれで動いていたなあという部分もある。しかしすっきりしたプログラムは読んでいても気持ちが良い。
.....................................................................................................................................
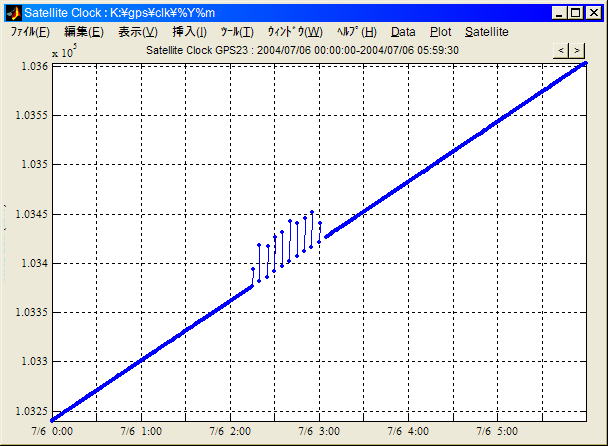
CODE CLKの異常値例(2)。2004/7/7 23:30-7/8
0:30 PRN24。線形補間IGS CLKとの比較 (衛星時計平均=0に正規化)。day
boundaryでたまにこの様な問題がある。この程度の異常はスタティックPPPでは殆ど影響はないがキネマティックPPPでは数十cmの誤差要因となる。やはりCODE
CLKは少し品質管理が甘い。こういうのを見ると人の作ったものをスクリーニングして使うほうが楽かか最初から自分で作るほうが楽かは結構微妙な所ではある。
Amazonで届いた参考書。
A.Bjorck, Numerical Methods for Least Squares
Problems, Society for Industrial and Applied
Mathematics 1996
最小二乗の数値解法についての専門書。rank
deficientな場合、制約付最小二乗、スパース最小二乗、逐次改良等についても詳説されている。6.9節にスパース最小二乗ソルバの精度,
実行時間比較がある。matlab標準ソルバ(スパースガウス消去法/LU分解)は悪条件の場合に精度、実行時間がかなり悪化する。スパースQRを使ったものが全般的に良いようだ。
.....................................................................................................................................
昨日記載の異常データ対応のためIGS-CODE-30s時計生成時に CODE CLKのQCを入れる様に改修。補間値が2ns以上外れた場合はアウトライアとして補間に使用しない様にした。色々と気をつけて補間をすればIGS-CODE-30s時計は十分に使える。この品質の30s時計を自分で長期間作るのはかなり大変なので30s時計についてはIGS-CODEで行く。1Hz時計は自分で作るしかないが。
何度も書いているが軌道にしても時計にしてもただ推定するだけならそんなに大変ではないが長期にわたって品質の良い推定値を安定に求めるのは本当に大変。あまり偉そうなことを言える立場ではないが、論文等は上手く行った結果だけを抜粋していることが普通なので実環境でその精度を出すのは色々な改良が必要。
.....................................................................................................................................
5月の地球惑星科学連合大会プログラム日程届く。持ち時間15分。少しピッチを上げてネタを作らねば。
タイトル(日本語) : 高時間分解能GPS/GNSS衛星時計推定とキネマティックPPPへの応用
タイトル(英語) : Estimation of high-rate
GPS/GNSS satellite clock and application
to the kinematic-PPP
講演セッション : D125 GPS
講演形態 : オーラル
講演日時 : 05月16日 16:15 - 05月16日
16:30
電子部品の通販リンク。わざわざ秋葉原まで出かけなくても今は通販で何でも手に入るのは有り難い。NovAtel
SuperStar II用にコネクタを少しとACアダプタ,
RS232C-USB変換アダプタ等注文。
RSオンライン
Degi-Key.com
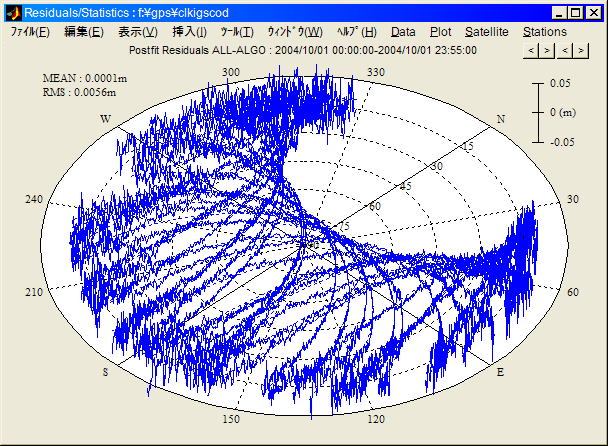
CODE CLKの異常値例。2004/7/6 2:30-3:00 PRN23。ファイル: cod12782.clk。IGS-CODE-30s時計によるLEO衛星PPPの誤差解析で見つけた。原因不明だが5分間隔値は正常なので時計補間の問題と思われる。これらをアウトライアとして自動で上手く落とせるといいのだが、このケースでは除外できず大きな測位誤差として現れてしまった。
.....................................................................................................................................
NovAtel SuperStar II GPS受信機+アンテナ届く。Fedexで頼んだら早いことは早いが$73もとられた。計$438 ($165+$200+$73)。StarViewというAPでコントロールできるらしいのでマニュアルと共にダウンロード。完全なOEMボードなので接続ケーブル等自作しなければならない。
.....................................................................................................................................
5月発表に向けて解析データの蓄積をしなければならないのだがどうも気が乗らないので、床に積んであるスペクトル解析、最適制御、適応フィルタ、デジタル信号処理、逆問題等々の参考書をパラパラ。特に適応フィルタはマルチパス推定/除去に使えると思うのだが上手い適用の仕方が思いつかない。多分広範な理論知識は長期的には有効なのだが、短期的には無駄に頭がこんがらがるばかりの様な気もする。
.....................................................................................................................................
rank deficientな観測方程式系を最小二乗で解く場合、単純には解けないので拘束条件を追加するか一般逆行列を使うのが普通である。それではカルマンフィルタで解く場合はどうすればよいか。カルマンフィルタの場合初期共分散が一種の拘束条件になるので何も対策しなくても解けてしまうのだが、その代わり推定値がうまく収束しない。精密測位の場合でも時計と搬送波位相バイアスは相互可換なので原理的に搬送波位相観測値のみでは時計及びバイアスは一意に決定できない。従って絶対値を求めるためには擬似距離観測値か何らかの拘束条件を入れてあげる必要がある。ただ擬似距離測定値を使うとDCBや擬似距離マルチパスに起因するバイアス成分により推定値にバイアス誤差が乗ってしまう。これはPPPの場合普通問題にならないが相対測位でバイアスを整数化する場合には問題になる(DCBは2重差で消去されるが)。GEONETの様に擬似距離マルチパスが十分に小さい場合は良いが通常ユーザ環境でのRTKの場合これがAR性能を悪化させている可能性がある。
キネマティックPPPの誤差を解析していてこの辺の問題が未だ残っていることに気が付いた。いまさらながら理論的な検討がおざなりだった様だ。ここは重要な所なのでちゃんと整理せねばならない。
論文、その他リンク
J.Dongarra, Freely Available Software for Linear Algebra
on the Web, May 2004
フリーの線形代数ソルバ一覧。ATLAS/BLASやLAPACK以外にも世の中には色々な行列ライブラリがあるものだ。案外Fortran9XやC++バインドのライブラリは少ない。でも未だに数値計算ではF77が主流というのは何とかしてほしい気がする。
.....................................................................................................................................
この時期の恒例、確定申告。混雑した申告会場に行く必要もないので最近はもっぱら郵送。予定通り半日で申告書を作って郵便局に行って出して終わり。
NovAtel OEM Superstar II Board
NovAtelの1周波GPS受信機ボードが結構安いことが分かったのでWeb注文。受信機ボード$165+小型アンテナ$235、計$400。当然測量用受信機に比較してマルチパス等の条件が悪いだろうが廉価1周波受信機+小型アンテナによるDGPSやRTKの評価に使う予定。GPS10ch
+ SBAS2ch、搬送波位相測定値1Hz出力。実際どの程度の精度が出るものか見もの。
.....................................................................................................................................
論文、その他リンク
M.Adlers, A Matlab Toolbox for Sparse Least Squares
problems, 2003
スパース最小二乗ソルバ。標準ではスパースQR分解を使っている様だがMatlab6.5.1では途中で実行エラーとなってしまう。
実用的な大規模問題ではスパース行列の取扱いが必須だが標準的な行列演算ライブラリでうまく取り扱えるものは多くはない。その点matlabはスパース行列の取扱いが優れており結構そのままでもいける。30000×100000の最小二乗もスパースにすれば(内部でどう解いているか分からないが)、\(backslash)で何とか解ける。ただスパース最小二乗も特定形式の計画行列の場合は形式毎に特別の解法がある様で専用のコーディングをした方が効率も良い様だ。
matlabの\の内部動作を調べてみた。matlabマニュアルによるとx=A\y;ではAの形式やフル/スパースによって以下の様に大変複雑な判定処理をしているよう。matlabマニュアルも線形問題の数値解法のよい参考になる。
(1) Aが三角: 前進後退代入
(2) Aが対称正定: コレスキ分解+前進後退代入
(3) Aが正方: ピボット付ガウス消去法によるLU分解+前進後退代入
(4) Aがフルで正方でない: HouseholderによるQR分解+最小二乗
(5) Aがスパースで正方でない: ピボット付スパースガウス消去法
(以上スパース行列の場合最小度合い並べ替えを含む)
.....................................................................................................................................
高速PPP解析ソフトに向け色々調査。時代はマルチコアなので折角だからOpenMPや並列化行列ライブラリを使う。言語はC(89)じゃなくてC99で行く。多次元配列がちゃんと使えないのはさすがにつらいから。もちろんC++という手もあるがC++はソースが綺麗に書き難いので嫌い。gccもC99準拠に近くなっている様なので可搬性も問題ないだろう。後は評価用に1台マルチコアPCを仕立てたいのだがIntel Core Duo用マザーがまだ手に入らないようだ。いまさらP-Dと云うのもなんだし新しいMac Miniを買うと言う解もある。
電離層モデルと電子密度分布(TEC)推定 解説資料追加。
.....................................................................................................................................
Amazonで届いた参考書
G.Strang and K.Borre, Linear Algebra, Geodesy,
and GPS, Wellesley-Cambridge Press, 1997
ざっとしか眺めていないが変な参考書。線形代数の基礎なのかと思っていると後半急にGPSのやたら詳しいモデルが出てくる。系統だった章構成になってないのであまり一般/初学者向けではない。まあ部分的には参考にはなる点はある。
.....................................................................................................................................
少し停滞。後2ヶ月で何をやるか考える。やはり高レートPPPの手法は色々な応用がきいて大変面白いと思うが理想にはまだまだ程遠い。
.....................................................................................................................................
論文、その他リンク
Y.E.Bar-Sever, A New Model for Yaw Attitude of Global Positioning
System Satellites, TDA Progress Report 42-123, 1995
GYM95と呼ぶJPLのGPS Yaw姿勢モデル。かなり古い論文でBlock
II/IIAのみが対象で多分Block IIRには当てはまらない。未だにNoon
Turnが何で何故起こるのかよく理解出来ていない。
前に「IGS FinalをCODE-30s時計を使って補間すると手軽にIGS品質30s時計が得られる」と書いたがそうでない場合があることが分かったので取り消し。IGS
Finalは単に高精度だけでなく、厳格な品質管理がされているせいで信頼性が高く悪データの混入が少ない。そのせいだと思うがIGS時計には短時間の抜けがあり下手な補間を行うと精度が悪化することがある。従って単純な補間でIGS品質が得られるとは言い難い。
.....................................................................................................................................
キネマティックPPPの長周期誤差がなかなか取れないので色々試す。どうも垂直は主に対流圏、水平はPCV+対流圏勾配が効いている様。GTには既に長期残差スタッキングによるPCV/マルチパス推定/補正機能があるのだが今まで殆ど使っていない。やっと使うことになるかもしれない。後は食衛星。これはかなり難しいがyawレート補正を入れるという手はある。でもJPLのyawレート推定値ってまともに使えるのだろうか。
.....................................................................................................................................
大規模最小二乗の数値解法について興味が出て検索していたら数値計算分野では色々な研究があるよう。どんどん脇道に逸れてしまいそうなので元に戻る。ただやっぱり正規方程式を使うのは安定性の面であんまり良くない様。反復改良とかを入れればよいのかもしれない。大規模問題の計画行列はほとんどスパースなのでスパースQRを使うという手もある。
大規模最小二乗に興味があるのはキネマティック測位を最小二乗で解こうとするとすると大規模問題にならざるを得ないからである。例えば1Hz-PPP 3H分でもパラメータ数30000、観測数100000位にはなる。位相バイアスや対流圏パラメータがあるのでエポック毎には解けない。その他TEC等でも時間変動パラメータの時間分解能を上げるとすぐ大規模問題となる。もちろんGTで実際やっている様にカルマンフィルタ/スムーザを使えばパラメータ数を減らして高速に解けるし実用的ではあるが最小二乗の意味で厳密解にはならない。特に短セッションの場合この近似誤差が無視できない精度劣化を引き起こしている可能性がある。ところで気付いたのだが後処理キネマティックでは皆厳密な最小二乗を解いているのだろうか。もし解いているなら結構大変な計算をしていることになる。
昨日の最小二乗数値解法実行時間計測プログラム。残差分散を出力させるように修正し再実行。正規方程式を使った解法でも14桁程度の精度は出ている。計画行列は乱数で生成しているので条件は良い。悪条件の場合はもっと悪化するのかもしれない。
>> testlsq
lsq1 : t=10.813 s=0.968878969802806
lsq2 : t= 5.047 s=0.968878969802811
lsq3 : t= 5.844 s=0.968878969802806
lsq4 : t= 5.032 s=0.968878969802801
lsq5 : t=11.750 s=0.968878969802807
lsq6 : t=46.250 s=0.968878969802813
lsq7 : t=53.187 s=0.968878969802796
PPP残差による搬送波位相マルチパス推定 (DRAFT) 追加。内容は少し乱暴かも知れない。例えばMALIの残差変動が本当にマルチパスが原因なのかは要解析。
1Hz-キネマティックPPPの位相残差を1恒星日ずらして並べたものの例(PRN27-IISC 上2004/12/25 下12/26)。マルチパスについて割と綺麗な相関が見られる場合もあるが単純なsidereal filterはむしろ短周期雑音が加算されるので相関の高い周波数領域のみバンドパスフィルタで取り出してから差し引く必要があるだろう。
.....................................................................................................................................
位相残差の3次元スカイプロット表示。IGS-CODE-30s時計によるスタティックPPP 24H分。こう見ると搬送波位相マルチパスの空間分布が良く分かる。
線形最小二乗数値解法の実行時間計測。パラメータ数1000、観測数5000。正規方程式を介した方が速いが演算誤差の影響を受けやすいので修正Gram-SchmidtやHouseholderによるQR分解を使う場合が多い様だ。ただ観測数が多くなると計画行列がメモリに乗らなくなるので大規模な問題は正規方程式を使わざるを得ない。パラメータ数が5000程度までは普通に解けるがそれ以上になると色々と工夫が必要になる。前にも書いたが最適化行列演算ライブラリの実行効率に追いつくのは至難の業なのでMKL等を使うのが現実的。ただLAPACKの使いこなしは難解。何か良い解説は無いだろうか。
| No. | matlab表現 | 実行時間(秒) | 備考 |
| 1 | x=H\y; | 10.796 | matlab任せ |
| 2 | x=(H'*H)\(H'*y); | 5.250 | 正規方程式+ガウス消去法 |
| 3 | x=inv(H'*H)*(H'*y) | 6.016 | 正規方程式+逆行列(LU?) |
| 4 | R=chol(H'*H); x=R\(R'\(H'*y)); | 5.234 | 正規方程式+コレスキ分解 |
| 5 | [Q,R]=qr(H,0); x=R\(Q'*y); | 11.844 | 計画行列QR分解 |
| 6 | [U,D,V]=svd(H,0); x=V*(D\(U'*y)); | 46.391 | 計画行列特異値分解(SVD) |
| 7 | x=pinv(H)*y; | 51.937 | 一般逆行列 |
.....................................................................................................................................
DGPSと単独測位の精度比較 (ユーザ局:三浦2, 基準局:つくば1, 基線長:113km, 24H)。電離層平穏期, 擾乱期。基線長100km以内であれば概ね水平RMSで50cm程度は確保できる様だ。後はマルチパスの削減。
球面調和関数の正規化係数については色々な流儀があるようでLegendre陪多項式も(-1)m付で定義されることがある。Pnm = (-1)mPnmと添字の位置で区別する場合も有るらしい。色々あるので係数を使う場合は関数の定義に気をつける必要がある。
GPS観測による対流圏ZTD推定値と数値予報モデルによるZTDの比較。2004年10月筑波。GPSはスタティックPPP。数値予報モデルは気象庁MSM。目的は数値予報モデルによる対流圏補正の精度評価。数cmの差が有るが傾向は良く一致している。長基線RTKやDGPSでは十分使える様な気がする。キネマティックPPPに使えるかは今後評価。
.....................................................................................................................................
| Home | by T.Takasu |