● : reduction on, ● : reduction off
(reduction=LAMBDA, search=MLAMBDA, Pentium 4 3.2GHz, Intel C/C++ 8.0+Intel MKL 7.2)
|
日記・備考録 |
2005 | 2006/1 2 3 4 5 6 7 8 9 10 11 12 | 2007 |
| December | January 2006 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
February | Home |
.....................................................................................................................................
Leick (3rd Edition)をざっと読む。統計学上の取扱いが煩雑で分かりづらくなっている箇所がかなりある。前にお勧めとは書いたがあまり一般向けでは無いのか知れない。でも最近の成果をきちんと網羅している参考書は他には無い。ところで単独測位解 7.4.2 closed solutionの導出が理解できない。どなたか理解された方教えて頂けません。
.....................................................................................................................................
昨日公開したRTKデモプログラムについて補足。単独測位に電離層フリー擬似距離を使っているため2周波観測値が必要で1周波で動く様にするためには電離層補正を追加する必要がある。精密測位にはL1のみしか使っていないため10km以上の基線では簡単にAmbiguity Fixしない。AR高速化のための2周波対応、サイクルスリップ検出、基準衛星切り替え、(中基線対応のための)電離層推定が必要な場合は要改造 (これらは良い課題)。その他問題点、不明点等ありましたらご指摘いただけると幸いです。
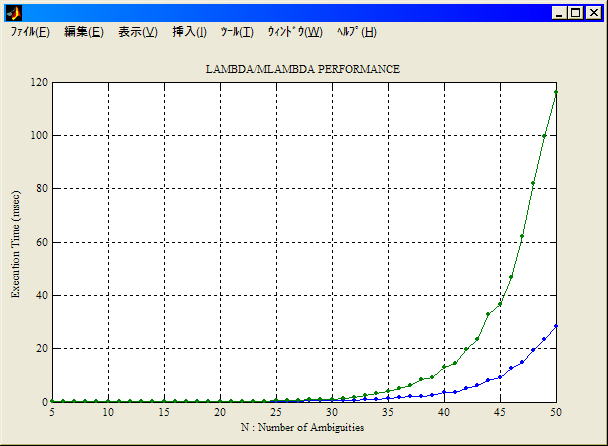
再度LAMBDA/MLAMBDA実行時間の評価。前処理(格子基底縮小変換)の有無で性能がどう変わるか。条件にもよるが一般的な単基線(n<30)では差は殆ど出ない。従って前処理を省略し探索のみの実装も有りだろう。でもこれって"Decorrelation"を行なわないからLAMBDAと呼べない。何と呼べばよいのだろう。

● : reduction on, ● : reduction off
(reduction=LAMBDA, search=MLAMBDA, Pentium
4 3.2GHz, Intel C/C++ 8.0+Intel MKL 7.2)
.....................................................................................................................................
精密測位の理論及び解析手法更新。RTKデモプログラム公開。m-fileだが他のライブラリを使っていずスタンドアロンで動く版。単独測位、RINEX読み込み、及びLAMBDA/MLAMBDA実装を含む。サイクルスリップ検出や基準衛星切り替えが入っていないし1周波のみなのでそのままではあまり実用的ではないがちょっと手を加えれば十分実用になる。基礎アルゴリズム確認用に開発したものなので一般公開。詳細はreadme.txt及びm-fileコメント参照。octave(2.1.x)+octave-forge環境でも動くが昨日書いたようにmatlabに比較し相当に遅い。そのうちRTKアルゴリズム解説を追加の予定。
.....................................................................................................................................
色々と思惑が有りmatlabで動いているm-fileをoctaveに移植。octaveも2.0系はセル配列が使えないようで2.1系が必須。cygwinにoctave 2.1.72+octave-forge(matlab互換ライブラリ)環境をインストールし動作確認。概ね修正しないでもそのまま動くようだ。ただgnuplotが正常起動しない。足りないライブラリとx-orgを入れてexport DISPLAY=localhost:0.0; startx &してやっとグラフが描ける様になった。でもoctave遅すぎ。何に時間がかかっているのか不明だがやたら実行時間がかかる。ATLASは入れていないが行列演算はそんなに使っていないので関係ないはず。基本性能を計測 (P4 3.2GHz, Win XP pro sp2)。
> a=0; tic, for n=1:1000000, a=a+1; end,
toc
elapsed_time = 1.156 (matlab 6.5.1 sp1)
ans = 22.766 (cygwin + octave-2.1.72)
ループや加算で10倍以上の性能差がある。これではちょっと使い物にならない。
.....................................................................................................................................
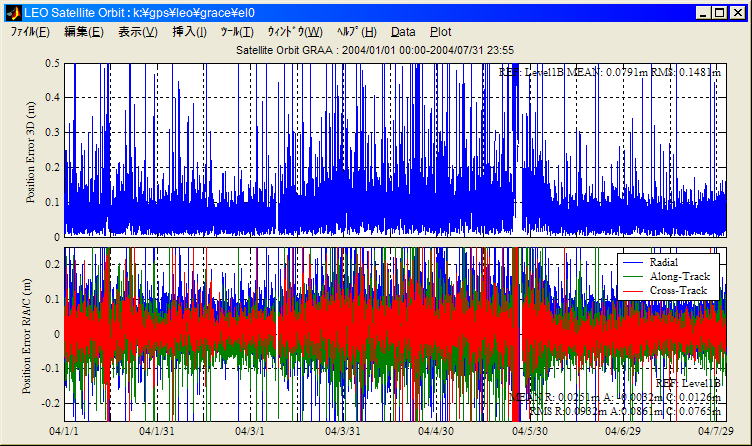
ALOSも上がったので随分前に行ったKinematic
PPPによるLEO衛星(GRACE-A) PODの長期評価結果を張っておく。2004/1/1〜7/31の7か月分。JPLのReduced-Dynamic解比較誤差である。条件はLEO POD頁と同じ。観測データは10秒間隔値が公開されているがIGS精密暦時計の時間分解能から5分間隔に間引いて推定している。前にも書いたがLEO衛星の場合アーク長が30分程度しか取れないので5分間隔推定は条件が厳しい。スパイク状誤差はサイクルスリップとday-boundaryにおける精密暦品質悪化が主な原因だろう。3月下〜5月末にかけての精度悪化原因は良く分からないがJPL解側の問題の可能性もある。Reduced-Dynamic解は運動モデルに依存するので太陽活動が活発化し大気密度変動が大きくなると精度が落ちる可能性がある。詳細不明だがGRACE搭載のBlackjack受信機は性能向上のため何度かファーム更新をしているらしいのでその辺が長期的な精度変化につながっている可能性もある。今後IGS品質30秒時計の作成とKinematic
PPPによるLEO POD評価をする予定だが5月の地球惑星科学連合に間に合うか。
30秒推定が可能になれば運動モデルを入れればより精度が上がる。500km以上の高度であればAir
Dragは最大10-4m/s2以下なので運動モデル誤差も数mm以下に抑えられるし対流圏は無視できるので理論的には1cm精度を狙えるはずである。
Amazonで届いた参考書
A.Leick, GPS Satellite Surveying 3rd edition, John Wiley & Sons, Inc., 2004
第2版は持っていたが内容が随分変わっているらしかったので注文。最近の成果が詳細まできちんと網羅されており秀逸。phase-windup,
phase center variationやdata snoopingについてもきちんと解説している。お勧めの参考書。ついでなので持っているGPS/GNSS関連参考書の短評を書いておこう。(Misra&Engeは翻訳版しか持っていない)
| 作者 | 書名 | 出版社 | 発行年 | 翻訳 | 短評 |
|---|---|---|---|---|---|
| B.Hofmann-Wellenhof, H.Lichtenegger | GPS Theory and Practice, 5th, Reviced Edition | Springer WienNewYork | 2001 | ○ | もはや古い |
| G.Seeber | Satellite Geodesy Foundations, Methods, and Application | Walter de Gruyter | 1993 | - | SLR, VLBIを含む衛星測地技術全般 |
| A.Leick | GPS Satellite Surveying, 3rd Edition | John Wiley & Sons, Inc. | 2004 | - | お勧め |
| G.Xu | GPS Theory, Algorithms and Applications | Springer | 2003 | - | 研究者向け |
| E.D.Kaplan (ed.) | Understanding GPS Principles and Applications | Artech House Publishers | 1996 | - | 少し中途半端 |
| B.W.Parkinson, J.J.Spilker Jr. (ed.) | Global Positioning System: Theory and Applications, Volume I,II | AIAA Inc. | 1996 | - | 解説論文集, もはや古いが内容は深い |
| P.J.G.Teunissen, A.Kleusberg (ed.) | GPS for Geodesy, 2nd Edition | Springer | 1998 | - | 解説論文集, 歴史的価値有り |
| P.Misra, P.Enge | Global Positioning System Signals, Measurements, and Performance | Ganga-Jamuna Press | 2001 | ○ | 一般向け, 信号/受信機関連詳しい |
| G.Strang, K.Borre | Linear Algebra, Geodesy, and Gps | Wellesley- Cambridge Press | 1997 | - | 測位で使う線形代数理論 (注文中) |
.....................................................................................................................................
論文、その他リンク
G.Gendt, switch to SP3-c format, IGSMAIL-5293, 23 Jan, 2006
来週から(IGU/IGRはGPS Week1360, IGSはGPS
Week1357から)IGS精密暦のフォーマットがsp3cに切り替わる通知。現在は従来のsp3形式と新しいsp3c形式の両者が提供されているが今後はsp3cのみになる模様。基本的にsp3cはsp3に上位互換性があるので通常問題にはならないが、対応していない解析ソフトはバージョンアップか変換が必要になる(参考IGSMAIL-5294)。ちなみにGTはver.0.5.4から既にsp3cに対応済みである。
.....................................................................................................................................
「だいち」(ALOS)打ち上げ成功, 地球観測利用推進センター EORC, JAXA, Jan
24, 2006
打ち上げ成功おめでとうございます。ALOSにはJAXAでは初めて2周波GPS受信機が搭載されこれにより精密軌道決定を行う。GRACEやCHAMPの様にGPS観測データと精密軌道が入手できればGTで評価してみたいが多分データは公開されないだろう。軌道決定そのものはGUTSで行うのだろう。公式資料では決定精度1mと言っているが測位技術は進歩しているので10cmを切らなければ公の場で発表するのは恥ずかしいだろう、と煽っておこう。しかしそれよりも何よりもまずはADEOS,
ADEOS-IIの様なことにならないことを願う。
.....................................................................................................................................
論文、その他リンク
T.Nagano et al., A Geometric Approach to Integer Ambiguity
Validation, ION GNSS 2005
"margin test"と呼ぶ新しいAR検定手法。シミュレーションで評価し、FIX時間及び信頼度でratio
testに比較し優れているとしている。筆者はmelcoの研究者の様。
.....................................................................................................................................
現行LAMBDAルーチンではn=50を超えると数値不安定が出てきて正常にreductionができない場合がある。reduction最初のLDLT分解でコケている様でpivotingも入れないとダメか。整数最小二乗もちゃんとした実装は結構大変。n=100程度までは実用時間で動くのを目標にしているのだが本当に可能かは良く分からない。
1/20に「格子基底縮小変換は多項式時間で解ける」と書いたがどうもLAMBDAやLLLで求めている格子基底縮小変換は最適解ではなく最適解の近似値なので多項式時間で解けるらしい。そしてより最適に近い変換を求めるアルゴリズムもある。Agrellのsemi-tutorialにはLLL,
KZ(最適に近い), 無変換の場合の最近格子点探索時間の比較がある。KZが最も良く次いでLLL,無変換の順であるがそれらの差はn=30ではそれぞれ1桁(10倍)くらいで案外大した差ではない。でもn=100では1000倍くらいになるはずなのでnが大きいところではより最適な変換が必須となる。
.....................................................................................................................................
LAMBDA/MLAMBDAルーチンの性能解析(評価プログラム)。nが小さいところでは十分速いがやはり実行時間は指数関数で効くようだ。従ってRTKではn=60程度すなわち3周波×20衛星くらいが実用限界か。複数基線の場合は基線毎に分割してFIXする必要があるだろう。厳密に言えばリアルタイムでは実行時間の上限を保証する必要があるので計算量がQの値に依存する整数最小二乗は使いにくいが、nが小さいところでは十分に実用的ではある。
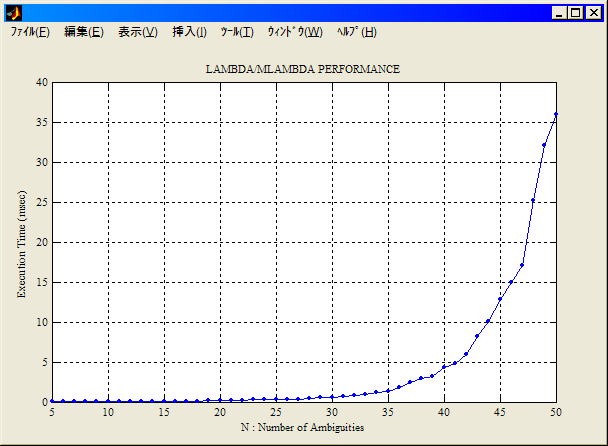
(reduction=LAMBDA, search=MLAMBDA, Pentium
4 3.2GHz, Intel C/C++ 8.0+Intel MKL 7.2)
整数最小二乗は多項式時間で解けるはずではと思って再度格子基底縮小の解説を調べてみる。どうも格子基底縮小変換そのものは多項式時間で解けるが、SVP(shortest
vector probrem)はNP困難で多項式時間では解けない様だ。従って格子基底縮小を使ってもnが大きくなるとすぐに整数最小二乗は実用時間では解けなくなるということになる。
もっとも逆に解けてしまうとSVPの困難性を利用している暗号も容易に解けるということになり困ってしまう。なおLLLアルゴリズムによる格子基底縮小変換を使ってこれらの暗号を攻撃する(すなわち計算量を減らす)のを"低密度攻撃"と言うらしい。
整数最小二乗の計算量は一般には次数の指数関数に従うが、実数解が整数格子点近傍に分布するという仮定を入れると多項式時間で解けるらしい。整数最小二乗も相当に奥が深い。富士通 近藤氏に問い合わせたら丁寧な回答と関連論文を送っていただいた。有難うございました。
論文、その他リンク
E.Agrell et al., Closest point search of lattices, IEEE Transactions on information Theory,
Vol 48, No 8, pp 2201-2214, 2002
近藤氏に教えて頂いた著名論文。AgrellのWebページから。格子基底縮小を使った最近格子点探索アルゴリズムに関するsemi-tutorial。どうも随分と横道にそれてかつ深みにはまりつつあるような気がする。下手をすると抜け出せなくなるかも。
.....................................................................................................................................
急に思いついて現行GT(ver0.6.1-alpha1)のソースラインカウントをとってみる。2005/05/10の結果と比較してみるとここ半年はたいしてコードを書いていないことが分かる。ちなみに現在、gpsestd.mのRevisionは93である。
m-file 22.1K, C-mex 5.9K (コメント除く)
論文、その他リンク
K.Kondo, The accurate optimal-success/error-rate calculations
applied to the realizations of the reliable
and short-period integer ambiguity resolution
in carrier-phase GPS/GNSS positioning, IEEE Transactions on Information Theory(preprint),
2005
GPS/GNSS測位における整数不定性決定(AR)成功/失敗率の精密計算。内容は統計学の基礎知識が無いとなかなかついていけない。なおarXivは物理, 数学, 天文学分野の論文サーバ。主にプレプリント。その他、物理,
天文学分野の論文DBではNASA ADS(Astrophysics Data System)が有名。最近は多くの論文がこれらサーバ等でオンライン公開されることが多いようだ。
.....................................................................................................................................
GT-RTKの精密暦対応。短中基線では放送暦より精密暦の方が精度が悪くなることがある。アンテナオフセットもちゃんと補正しないといけないかもしれない。
.....................................................................................................................................
昨日のpull-in region描画でeuclid距離のVoronoi図を求めるのはmatlabのvoronoi関数を使っているのだが自前でVoronoi図をを求めるのは結構複雑なアルゴリズムが必要になるようだ。これは計算幾何学と呼ばれる分野の問題の一つである。
腰塚編, 計算幾何学と地理情報処理 第2版, 共立出版, 1986
随分と昔に購入した参考書だが有用なアルゴリズムが多数掲載されていて時々調べることがある。Voronoi図についてもかなりの頁を使って詳説されている。今回の問題もよく調べてみると4.8.3(3)の項に説明がある。
χ2分布の上側確率点(n:自由度,α:有意水準)の求め方。
(1) χ2分布の上側確率関数: Pn(x)=1-γ(n/2,x/2) (γ:
不完全gamma関数)
(2) 2分検索によりPn(x)=αとなるxを求める。
計算ルーチン例と結果(α=0.995-0.005,n=1:10)。
n:a 0.995 0.990 0.975 0.950 0.900 0.500 0.100 0.050 0.025 0.010 0.005 1: 0.000 0.000 0.001 0.004 0.016 0.455 2.706 3.841 5.024 6.635 7.879 2: 0.010 0.020 0.051 0.103 0.211 1.386 4.605 5.991 7.378 9.210 10.597 3: 0.072 0.115 0.216 0.352 0.584 2.366 6.251 7.815 9.348 11.345 12.838 4: 0.207 0.297 0.484 0.711 1.064 3.357 7.779 9.488 11.143 13.277 14.860 5: 0.412 0.554 0.831 1.145 1.610 4.351 9.236 11.070 12.832 15.086 16.750 6: 0.676 0.872 1.237 1.635 2.204 5.348 10.645 12.592 14.449 16.812 18.548 7: 0.989 1.239 1.690 2.167 2.833 6.346 12.017 14.067 16.013 18.475 20.278 8: 1.344 1.647 2.180 2.733 3.490 7.344 13.362 15.507 17.535 20.090 21.955 9: 1.735 2.087 2.700 3.325 4.168 8.343 14.684 16.919 19.023 21.666 23.589 10: 2.156 2.559 3.247 3.940 4.865 9.342 15.987 18.307 20.483 23.209 25.188
現在GT-RTKのAmbiguity FIX判定に最も簡単なratio test(閾値パラメータ=2)のみを使用しているのだがたまにミスFIXを起こす。AR検定手法のサーベイを行っているのはこの改善のため。あとAmbiguityのpartial fixingにも興味があるがこれはなかなか文献が無い。
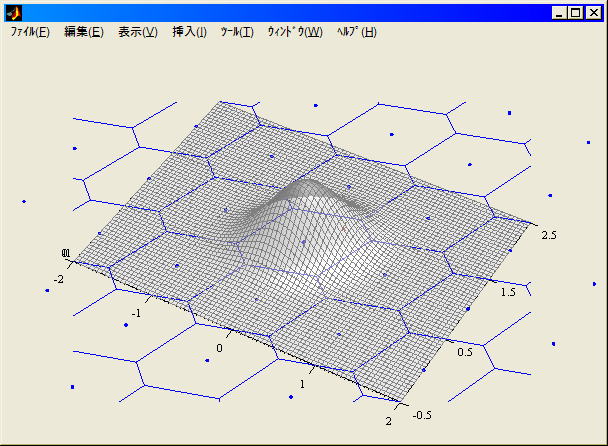
Z変換後のAmbiguity探索空間におけるprobability
density function P(z)=1/sqrt(det(Q)*(2*pi)^n)*exp(-1/2*(z-zn)'*Q^-1*(z-zn))、といってもこの場合単なる二次元正規分布。ARのsuccess
rateやfail rateをちゃんと求めるにはこの関数を領域内積分するが厳密に求めるのは難しいのでモンテカルロ積分を使うのが一般的なようだ。
.....................................................................................................................................
覚え書き
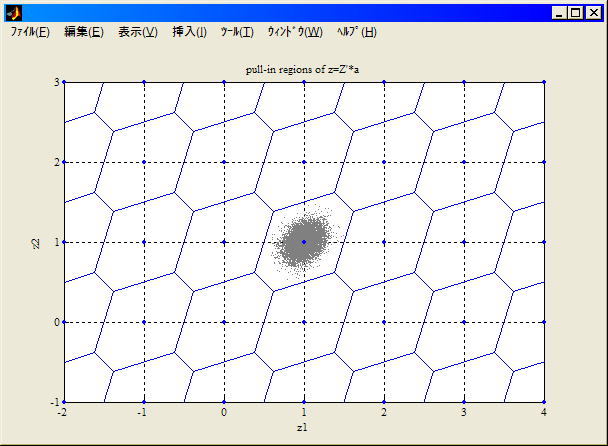
integer least-squareの二次元pull-in region描画法。整数格子点を共分散逆行列のcholeskeyで変換しvoronoi図を描いてから逆変換して戻せばよい。ちょっと苦労したが出来てしまえばなんてことはない。LAMBDA
Z変換後pull-in region表示プログラム例と結果。
何故これでよいかは以下の通り。(zn: 整数格子点,
Rn: zとznの距離二乗, Q: zの共分散行列)
Rn(z)=|z-zn|2Q=(z-zn)'*Q-1*(z-zn)=(z-zn)'*L-1*L'-1*(z-zn)=x'*x=x12+x22+... (L=chol(Q), x=L'-1*(z-zn), z=zn+L'*x)
.....................................................................................................................................
論文、その他リンク
H.Konno et al., Analysis of Ionosphere Gradient Using Japan
GEONET Data, ION NTM 2005
GEONETデータを使った日本域上空の電離層遅延勾配の解析。解析手法や磁気嵐時の解析結果について紹介している。精密測位の面から見れば滑らかであれば電離層遅延勾配が大きくてもそれほど問題にならない。むしろシンチレーションの様に細かい変動を引き起こす現象の方が取扱いがやっかいである。いずれにしてもRTKにとっても電離層推定/予報の高精度化はキーとなる技術の一つであり今後いっそうの進展を望む。
.....................................................................................................................................
論文、その他リンク
S.Verhagen, Integer ambiguity validation: an open problem?, GPS Solutions 8(1):36-43, 2004
整数不定性決定(AR)検定手法のサーベイと評価。$30也。ARにおいて整数最小二乗解は(誤差がgaussianである前提で)最適解を与えるが必ずしもその解をそのまま採用してよい訳ではない。それは解の中にはある確率で不正解(すなわちミスFIX解)が含まれるからである。従って整数最小二乗の後に解の検定(validation)を行い信頼できない解の場合はそれを採用せずFLOATのまま取り扱うことが行われる。現在各種検定手法が存在するがその理論的背景が曖昧なものが多い。またこれらの手法は経験的な閾値パラメータを含みそのパラメータの決定方法は必ずしも明確でない。本論文ではAR検定手法につき各種手法を紹介し、シミュレーションにより評価している。手法比較に関する結論は曖昧であるが各手法を概観するには良い。F-ratio
testとratio testは異なる手法であることを始めて知った。
P.Teunissen et al., On the Foundation of the Popular Ratio Test
for GNSS Amibuity Resolution, ION GNSS 2004
AR検定で最もよく使われるratio test(最適解と次善解の残差二乗和比を検定に使う)の評価。その中で最適IA推定
(Optimal Integer Aperture Estimator) を提案している。最適IA推定は指定不正解率以下の領域を整数引き込み領域(pull-in
region)とするもの。ratio testと最適IA推定を比較しその性能を評価している。結論としてratio
testの性能は最適IA推定に近いが閾値パラメータは固定値ではなくは所要不正解率から算出した値を使用する必要があるとしている。
覚え書き
AR検定でF分布の棄却域(critical value of f-distribution)
Fα(n,m) (n,m:自由度, α:有意水準)を求める必要がある。
この値の求め方。
(1) F分布の上側確率関数: Fn,m(x)=1-I(n*x/(m+n*x);n/2,m/2)
(I: 不完全beta関数) (参考)
(2) 2分検索によりFn,m(x)=αとなるxを求める。
計算ルーチン例と結果(α=0.05,n,m=1:10)。
m n 1 2 3 4 5 6 7 8 9 10 1: 161.445 199.531 215.703 224.609 230.156 233.984 236.797 238.906 240.547 241.875 2: 18.513 18.999 19.165 19.248 19.297 19.331 19.353 19.370 19.385 19.395 3: 10.128 9.552 9.276 9.117 9.014 8.940 8.887 8.845 8.812 8.785 4: 7.709 6.945 6.591 6.388 6.256 6.163 6.094 6.041 5.999 5.964 5: 6.608 5.786 5.410 5.192 5.050 4.950 4.876 4.818 4.772 4.735 6: 5.988 5.143 4.757 4.534 4.387 4.284 4.207 4.147 4.099 4.060 7: 5.591 4.738 4.347 4.120 3.972 3.866 3.787 3.726 3.677 3.636 8: 5.317 4.459 4.066 3.838 3.687 3.581 3.500 3.438 3.388 3.347 9: 5.117 4.257 3.863 3.633 3.482 3.374 3.293 3.230 3.179 3.137 10: 4.965 4.103 3.708 3.478 3.326 3.217 3.135 3.072 3.020 2.978
.....................................................................................................................................
Proceedings of the 17th International Technical
Meeting of the Satellite Division of The
Institute of Navigation, ION GNSS 2004
Proceedings of the 16th International Technical
Meeting of the Satellite Division of The
Institute of Navigation, ION GPS/GNSS 2003
追加注文したION GPS/GNSS 2004, 2003の講演論文集CD-ROM届く。IONメンバ$115/CD也。論文もいい加減飽きてきた。実装の方は止まったままで次に何をやるか迷っている。
.....................................................................................................................................
論文、その他リンク
D.Kim et al., GPS Ambiguity Resolution and Validation:
Methodologies, Trend and Issures, 7th GNSS Workshop - International Symposium
on GPS/GNSS, 2000
各種AR手法の概説、クラス分け及び比較。トレンドと現時点での課題。AR手法の研究状況をざっと概観するには良いが内容は薄い。
.....................................................................................................................................
SCPNT: Stanford Center for Position, Navigation
and Time
スタンフォード大SCPNT Webサイト。もともとはGPSLABと呼ばれていた研究所。WAAS,
LAAS, 着陸支援システムの研究が主体。
年が明けたのにちゃんと今後の研究開発のテーマを整理せずずるずると来ているのでここでまとめておこう。
(1) 長期(1年〜数年)
・GT解析モデル改良及びエンジンC化、高品質化→ver.1.0化
・GT-PPP(仮称)の開発、公開。
・GT-RTK(仮称)の開発、公開。
(2) 短期(1ヶ月〜数ヶ月)
・RTK技術整理
・ネットワークRTK補正情報生成(電離層,対流圏)
・高時間分解能衛星時計補間
・新IGSアンテナモデルの評価
・地球惑星科学連合講演会発表
論文、その他リンク
W.Gurtner, RINEX Version 2.11, IGSMAIL-5288, 11 Jan., 2006
RINEXの新バージョン(ver.2.11)。旧バージョン(ver.2.10)からの主な変更点はGalileo/近代化GPSの追加コード/搬送波対応、SBAS
GEO NAVの追加等。2桁の観測データコードではデータ種別の十分な識別が出来ないので次期RINEXバージョン(ver.3)ではこのフィールドの拡張が計画されている様だ。
.....................................................................................................................................
MGP's Electronic Library
TeunissenのMGP関連の論文検索。Author=Teunissenで検索するとなんと176件の論文がHitしかつその多くがオンラインで閲覧できる。多分LAMBDAについてのオリジナル論文はほぼ網羅されているのではないか。それにしても凄い量産ぶりである。
P.Teunissen et al., A Comparison of TCAR, CIR and LAMBDA GNSS
Ambiguity Resolution, ION GPS 2002
上の論文のうち比較的新しいものから。Galileo(E1,E2,E4)/近代化GPS(L1,L2,L5)の3周波観測値によるAR手法の性能比較。TCAR(Three-Carrier
Ambiguity Resolution)及びCIR(Cascading Integer
Resolution)は共にinteger-bootstrappingと呼ばれる手法。TCARはE1-E2(10.47m),
E1-E4(0.90m), E1の順で、CIRはL2-L5(5.86m),
L1-L2(0.82m), L5の順で順次整数丸めによりAmbiguityを整数化する。TCAR,CIR,LAMBDAの性能を単一エポックのAR成功率(success-rate)で評価しLAMBDAが優れているとしている。LAMBDAの様なinteger
least-square法は一般には整数最小二乗の意味で最適解を与えるから以上の結論は当然である。ただしLAMBDAの様な全Ambiguityを同時FIXする手法はどれか1つのAmbiguityの推定精度が悪いとそれに引きずられて全AmbiguityがFIXしなくなることがある。その点intger-bootstrappingは衛星(ペア)毎にAmbiguityが独立になるためよりrobustな推定手法であり単純に劣っているとは言えない点もある。
.....................................................................................................................................
寒い。昨晩は-11度、今日の昼間で-4度。PCの廃熱で暖かいはずなのに全然部屋の気温が上がらない。足元が冷えて仕方ないのでコタツで論文読み。
.....................................................................................................................................
論文、その他リンク
I.Kashanai et al., The Double Difference Effect of Ionospheric
Correction Latancy on Instantaneous Ambiguity
Resolution in Long-Range RTK, ION 2004
長基線RTKにおける電離層補正に関する研究。長基線RTKの瞬時ARには二重差電離層遅延精度5cmが必要。基準局網による60秒遅れの電離層予報値(の補間)で100%の瞬時ARが可能としている。ION
2004のbest paper award。
Commission 4: Positioning & Applications
Sub-Commission 4.5: Next Generation RTK,
Working Group 4.5.1: Network RTK, International Assosiation of Geodesy
IAG(国際測地学協会)のネットワークRTKワーキンググループサイト。ネットワークRTKの概説が参考になる。ReferenceにネットワークRTKに関して重要な論文のリンクが張られている。基準局網を使った補正を含む中長基線RTKは、現在まだ技術的に確立した分野ではなくやることが沢山残っている様だ。さてどこから手をつけるか。
ぼちぼちと基準局網による電離層補正を始めているのだがなかなか上手く行かない。GT-RTK(仮称)も改良を加えて短基線では概ね実用に近くなって来たのだが中長基線ではやはり難しい点が多い。あたりまえだが何事も簡単には行かない。
地球惑星科学連合2006年大会, May 14-18, 2006
予稿集原稿受付: 1/10〜2/8。昨年5月,10月と連続して発表しているので今回もGPSセッションに何か出したいと思っているがまだ良いネタが無い。できれば長基線RTKか高時間分解能PPPで出したいのだが。地球惑星科学連合合同大会の1999-2005予稿集からGPS関連セッションの内容を一通り見る。日本の衛星測位技術研究の層の薄さを実感する。
.....................................................................................................................................
NTRIP Symposium & Workshop on Streaming
GNSS data via Internet, 6-7 February, 2006
2006/2/6-7に開催されるNTRIP(Networked Transport
of RTCM via Internet Protocol) に関するシンポジウムWebサイト。NTRIPはGNSSデータのインターネットを介したストリーミング放送の規格であり2004/9にRTCM標準の一部となった。送信するGNSSデータにはDGPS補正データ,
RTK補正データ, WAAS補正データ, 生観測データ,
SP3軌道情報, RINEX観測データ等が含まれる。既にNTRIPを使ってリアルタイムGNSSデータ放送(RAW,DGPS,RTK等)を始めているサイトもある様だ。(日本には未だない様でいつもの様に世界から取り残されている)。既にフリーのNTRIP実装もあるし商用ソフトでサポートしている例もある。IGS観測局の観測データがNTRIPを使ってリアルタイム配信される様になると誰でもリアルタイム精密軌道・時計決定が可能になるだろう。日本でもGEONETデータがこの様な仕組みを使って一般に公開されることを望むが、現状データ配信自体がビジネスになっているので、色々と難しい点が多いかもしれない。
.....................................................................................................................................
European Space Agency, First Galileo satellite on orbit to demonstrate
key technologies, 28 December 2005
初のGalileo実証衛星Giove A、2005/12/28 05:19UTCにロシア
バイコヌールからソユーズにより打ち上げ。この衛星はSTB-V2/A
(Galileo System Test Bed Version 2) と呼ばれていたもの。2台のルビジウム時計及び2台のGalileo測位信号発生器を搭載し軌道上実証を行う。この後PHM
(パッシブ水素メザー) 時計を搭載したGiove
B、そして4機の運用衛星を打ち上げ軌道上検証(IOV)を行う。それから残りの衛星を打ち上げFOC
(Full Operational Capability) に移行するとしている。とうとうGalileoも本格的に動き出した様だ。
.....................................................................................................................................
新年あけましておめでとうございます。本年も昨年同様にご愛顧よろしくお願い申し上げます。
.....................................................................................................................................
| Home | by T.Takasu |