|
日記・備考録 |
2005 | 2006/1 2 3 4 5 6 7 8 9 10 11 12 | 2007 |
| May | June 2006 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
July | Home |
.....................................................................................................................................
しかし東京は暑い。特にこちらの夜の涼しさは格別。そろそろ蛍の飛ぶ頃。
.....................................................................................................................................
地震波観測等にGPSを使う場合、絶対座標より相対変動を取りたい場合が多いので短周期のノイズが小さい事が重要である。この点PPPは基準局の受信機雑音/マルチパスの影響を受けないので相対測位に比較し有利である。ただしPPPは精密暦時計ノイズ、及び電離層フリー線形結合によるノイズ増加(単一搬送波の3倍)の影響を受けるので、結局中長基線相対測位より少し良い位の所に落ち着く。ただし衛星時計や電離層遅延はある程度の時間相関を仮定できるのでフィルタによりこれらのノイズを低減する事は可能なはず。絶対座標誤差や長周期ノイズはこれでは落とせないがうまく行けば短基線相対測位に近いところまで行く可能性がある。秋の測地学会はこの辺のテーマでいくかな。
.....................................................................................................................................
現行GTはエラー終了した際にいちいちデバッガで追わないと原因が分からないことがある。この辺のエラー処理や使い勝手の改善。一般ユーザリリースに向けての整備。
.....................................................................................................................................
昨日と同じ条件で暦だけ精密暦にした結果 (P1-C1補正未、補正済)。通常の単独測位では放送暦の誤差に隠れてあまり差が出ないが結構大きく効いている。ついでにP1-C1補正+キャリアスムージングの結果。この辺になると段々とPPPに近くなる。残りの誤差要因は、潮汐、対流圏、スムージング時の位相バイアス項。概ね理論通りの精度が出ており単独測位アルゴリズムそのものは問題なさそうだ。
.....................................................................................................................................
TGDの件、DGPSでの取り扱いはどうなっているかRTCM SC-104 (v.2.3) を調べてみた。Msg Type 1がGPS用PRC (疑似距離補正)の規定だがやはりP1-C1バイアスの記述はない。PRCは単純なTGD補正後の疑似距離に対する補正量としているので、PRCにはP1-C1バイアス補正を含むということになる。
なおRTCM Msg Type 1 PRCの補正は、a.受信機時計誤差, b.TGD, c.衛星時計誤差, d.相対論補正のみ修正した疑似距離観測値に対し行うとしており(4.3.1)、対流圏/電離層遅延は(モデルで)補正しては**いけない**。すなわちPRCには全対流圏/電離層遅延補正が含まれる。これは基準局とユーザの補正モデル不一致による誤差増大を避ける意味だろう。RTCMにもやはり信号送信時の衛星位置の求め方がきちんと規定されていない。基準局/ユーザ共に同じメーカの受信機であれば問題ないが、異なるメーカの受信機間DGPSではこれらのアルゴリズム解釈の違いによる精度劣化の可能性を否定できない。
さてP1-C1バイアス補正は本当に単独測位精度に効くのかやってみた。(結果:
補正未、補正済)
電子基準点960759 三浦2。2005/4/2 0:00-12:00GPST。モデル誤差を低減するため電離層遅延は2周波疑似距離から推定しスムージングをかけて補正している。搬送波位相観測値は使用していない。対流圏は標準大気+Saastamoinen。P1-C1バイアスはIGS推定値を使用。明らかに有意の差がある。
.....................................................................................................................................
6/23はアストロの講演申込〆切なのだが今年はちょっと無理。あと1ヶ月強で30分話す内容を揃えるのは今の状況ではきつい。今年の予定は、あと秋の測地学会(10/18-20,水沢)とGPS/GNSSシンポ(11/15-17,東京)くらい。ほぼ完全に1人でやっているので少し他の仕事が入り出すと研究開発にさける時間は限られてしまう。まあボチボチと地道にやっていこうと思う。
昨日書いたTGDの補足の補足。測位の面だけ考えると実はTGDの値は絶対値である必要はない。すなわち衛星間のTGDの相対値がちゃんと定まっていれば測位解に誤差要因として現れることはない。実際TGDを米国DoDがどう決定しているかよく分からない点が多いのだが、どうも衛星打上前の精密計測で初期値を求め経年変動は実際の観測値を使って推定しているらしい。2周波のコード観測値には異なる電離層遅延がのるし受信機にも衛星と同じようにコード間遅延差(DCB)が存在するので、適当な電離層モデルと多数局の観測値を使って全パラメータを同時推定している可能性が高い。原理的には1つの基準受信機DCBが正確に決定できれば全DCBの絶対値も決定できるはずであるがその様な方法で絶対DCBを決めているかどうかは分からない。なおCODEやIGSのDCBは相対値でありTGDと同じ基準で決定されている訳ではない。この点昨日の説明図にはウソがある。回路遅延やケーブル遅延には温度依存性があるのでTGDも時間的に安定かどうかは不安であるが普通は短期では一定であると扱う。ただ食期間等の衛星温度変動が大きくなる時期にはTGD変動に伴う測位精度低下の可能性は否定できない。なお受信機DCBの日周変動は割と大きく一定であるとするのは無理があるとする報告もある。(ただこの変動は測位では受信機時計推定値に吸収されるので通常考慮する必要はない)
TGD(群遅延時間)という名前は明らかに電離層による群遅延と混同されやすいので呼称として適当でない。昨日書いた様にTGDは衛星内部のコード遅延間の差を表すパラメータであり、電離層遅延とは直接は関係ない。
E.D.Powers et al., Absolute Bias Estimation of the GPS Satellite
Timing Group Delay (TGD) Using Calibrated
GPS Monitor Receivers, ION GNSS 2006
まだアブストしかないがJPLによる絶対TGD推定とそれを使ったUTC(USNO)-GPST接続についてION2006で発表があるらしい。コードバイアス絶対値は測位には影響なくても時刻決定には効くので時刻決定には複雑怪奇でややこしい話がたくさん有る。例えば昨日の説明ではアンテナ位相中心が存在することを仮定していたが、現実にはその定義は簡明ではない。定義が難しいものを基に定義された時計はもっと定義が難しい。時計の話は厳密なことを言い出すと収拾がつかなくなるのであまりつっこまないでいるができればどこかできちんと整理したい。
.....................................................................................................................................
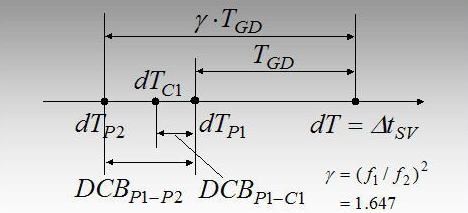
6/15に書いた単独測位計算の注意を読み返してみてTGDの説明が分かりにくいと思うので補足説明しておく。まず航法メッセージのSV Clockパラメータを係数とした2次式で表される衛星時計誤差が何を表しているかを理解する必要がある。この時計誤差は搭載原子時計と(真の)GPS時刻との差を表している**のではない**。この時計誤差は測位信号が衛星アンテナ位相中心を出発する(真の)GPS時刻と測位コードに刻印された時刻との差を表す。測位コードに刻印された時刻は搭載原子時計を基につけられるが、測位信号が衛星アンテナ位相中心に達するまでに電子回路やケーブルを経由するから、その遅延分だけ(実際の)搭載原子時計の時計誤差からずれていることになる。この遅延は一般に測位コードによって異なるので、どの測位コードで測るかで衛星時計誤差の値が異なるという一見奇妙なことになる。そして時計誤差はP1, P2コードで測られた時計誤差の電離層フリー線形結合で表し、1周波ユーザはその差分をTGDパラメータで補正する、というのがGPS航法メッセージの流儀である。6/15に書いたように厳密にはP1-C1間にもこの遅延差があるが、GPS-ICD (ICD-GPS-200C) ではTGDについて以下の様な書き方をしており、L1についてC/A, Pコードのどちらのコードを使った値かは曖昧である。ただ実際のTGDパラメータ値を確認すると明らかにPコード用補正値なので一般のC/AコードユーザはTGDに加えP1-C1バイアスの補正が必要となる。
> 20.3.3.3.3.2 L1-L2 Correction. The L1
and L2 correction term, TGD, is initially
calculated by the CS to account
> for the effect of SV group delay differential
between L1 and L2 ..., Thus, the user who
utilizes the L1 frequency
> only shall modify the code phase offset
in accordance with paragraph 20.3.3.3.1 with
the equation...
これらの関係が分かりにくいので図を示しておく。ただプラスマイナスは定義によっては反対になることがあるのでその都度確認が必要。

.....................................................................................................................................
名大でのセミナーに参加。主に地殻変動観測にGPSを利用されている研究者の方々にHR-PPPやGTの紹介。色々と貴重なご意見も聞かせて頂いて大変参考になった。
.....................................................................................................................................
明日のセミナーの準備。いつの間にかプレゼン資料はたまってきたのでそれを流用するとして、聞きに来られる方の興味を引きそうなネタを少し用意。ホントはHR-PPP論文を仕上げてからにしたかったのだけれど。でもいい機会なので実地でGPSを使われている研究者のご意見を色々と聞いてこよう。
.....................................................................................................................................
6/10の記述に計算ミス。mmとcmを間違えている。計算で桁を間違えると結論が全然異なるので話にならない。トシかな。
.....................................................................................................................................
時間が過ぎるのが速い。やるべきことがスタックしているのに全然捌けない。
> 単独測位計算については誤解や間違いが多すぎるので、ちゃんとした解説をそのうち公開予定。
5/31に以上の様に書いたがちゃんとまとめる時間がなくなりそうなので、これから単独測位計算を勉強したいと思われている方のために参考書に殆ど書かれていないが注意すべき点を以下に簡単にまとめておく。疑問点、不明点等有れば遠慮なく問い合わせ下さい。
(1) 信号送信時の衛星位置計算。内容は6/1、6/3に書いたとおり。まずここで躓く方が非常に多い。
(2) TGD補正。TGD補正を行わないのは論外だが、航法メッセージ中のTGDは(GPS-ICDには明記されていないが)P1ユーザ用の補正値である。すなわち航法メッセージの衛星時計はP1-P2電離層フリーで定義された時計である。従って一般のC/AコードユーザはTGDに加え衛星P1-C1バイアスの補正が必要である。P1-C1バイアスは別途推定値を手に入れる必要がある。一般にはCODEかIGS標準解析使用値を使えば良い。この効果は大きな衛星で50cmくらいの誤差を生じる。(なおDGPSではPRCにこれらの補正も含まれてしまうので普通この補正の必要はない)
(3) ガウスニュートンで非線形最小二乗を解く場合が多いが、その際観測データに異常データが含まれていると収束しない場合がある。また電離層遅延、対流圏遅延モデルが逐次近似の途中で異常値を吐くと収束しないことがある。この件はどう対応するのが最適かはよく分からないが、事前/事後残差チェック等のQCやRAIMアルゴリズムを導入する必要がある。
(4) 放送暦はGPS-ICDでは衛星アンテナ位相中心位置で定義されると書かれているが、実際放送暦とIGS精密暦+アンテナオフセットを比べてみると明らかにラジアル方向に1m程度のオフセットがある衛星が存在する。この件は長期でちゃんと評価したわけではないので確かなことが言えないが本当にアンテナ位相中心の値かは少し疑問がある。これについては今後調べてみたい。
GPS/GNSSシンポジウム2006, 日本航海学会GPS研究会/東京海洋大海事交通共同研究センター
秋のGPS/GNSSシンポの開催通知がupされている。11/15-17。予稿〆切9/10。第1回GPSロボットカー学生コンテストが予定されている。GPSを航法センサに使った自律ロボットカーレース。技術的には色々と工夫のしがいがあって面白そう。
ION GNSS 2006, The 19th international technical meeting
of the Institute of Navigation Satellite
Devision
ION 2006のプログラム及びアブストがupされている。9/25-29。米国テキサス州フォートワース。PPPセッションだけざっと見てみたがデシm級RTK応用が主流で、あまりcm/mm級の精密解析に使うというのはない。リアルタイムでは結局相対測位RTKやVRSとの勝負になるのでなかなかPPPの優位性を見いだせる応用は多くないような気がする。リアルタイムPPPは次の研究テーマ候補の一つだがARのできないRTK-PPPで相対測位RTKに近い精度まで持っていくのは簡単ではない。単独測位に対するDGPSと同じようにPPPに対するDGPS-PPPと言うのはもちろん考えられるのだが。さて次はどうしようか。
.....................................................................................................................................
搬送波位相測定値による精密測位の理論及び解析処理 更新。6/10に書いた精密暦衛星時計安定度の件の修正。
.....................................................................................................................................
The Allan Variance
Allan varianceの定義。D.W.AllanのwebサイトAllan's Timeから。色々と時刻や時計に関する解説があり参考になる。"Allan
deviation"と言うとAllan varianceの平方根をとるだけでいいはずだが、ちゃんとした定義を見たことがない。多分これで問題ないと思うが。
.....................................................................................................................................
> 一部誤解があり、解説には少し省略があるがプログラム自体はノバテルであれば問題ないことを確認した。
6/8に書いた以上の件につき質問があったので補足。ノバテルの場合(多分デフォルトでは)受信機時計を連続的にGPSTに合わせるタイプの受信機なので受信機時計誤差は無視できる。従って電波伝搬時間=疑似距離/C+衛星時計誤差で求めることができるので、光差方程式を解く必要はない。一般の受信機では受信機時計誤差を無視できないので光差方程式を解く必要がある。基本の観測方程式が頭に入っていればすぐ理解できるはず。しかし色々な近似が入っているので全部が問題ないことを確認するのは結構大変。
測位計算時の衛星時計誤差の取り扱いにつき問題発見。6/1に衛星位置計算時に"dT(ts)の代わりにdT(tr)を使っても問題ない"と書いたが(これ自身は正しいが)、測位計算時に衛星時計誤差としてdT(tr)を使って良いわけではない。現在大きな衛星で6×10-11程度の時計ドリフトがあるのでdT(ts)の代わりにdT(tr)を使うと
6×10-11×0.07×3×108=1.2cmmm(訂正: 6/16)程度の誤差を生じる。これは精密単独測位では無視できない。精密測位の理論と解析処理 A.4.2.3で以下のような記述があるがこれは間違い。
> 精密暦の衛星時計誤差は GPS時刻に同期した値が与えられるが、測位計算で必要となるのは測位信号送信時刻の値であり
> 精密暦の時刻とはずれがある。ただし0.1
sec程度の時間内では衛星時計は十分に安定であると考えられるのでその程度の
> 時刻差であれば近い時刻の精密暦の値をそのまま使用しても誤差は無視できる。
時計安定度は普通ドリフトを除いて定義されるが、これを書いた時は時計安定度と時計ドリフトをごっちゃにしている。正しくは精密暦時計を引く際に送信時刻の値に補間あるいはドリフト補正をしなければならない。現行バージョンGTには多分この問題に起因する若干の精度悪化がある(削除: 6/16)。しかし時計の取り扱いは本当に難しい。
.....................................................................................................................................
IRISのSEEDリーダRDSEED4.6をダウンロードしてcygwin上でmake。注意は2点。
(1) rpcライブラリが無いと構築失敗するのでlib-sunrpcをインストール。リンクオプションは
-lrpcにする。
(2) rdseed.c 2750: strupr()がcygwinのstringライブラリと衝突するのでコメントアウト。
やりたいのはseedフォーマット中のpoles and
zerosデータを吐き出させること。これを使ってSACのtransferコマンドで地震計応答特性の補正を行う。しかしどうもSACがちゃんと動かない。cygwin上でmakeした版ではダメかも。多分Linuxならちゃんと動くだろうけど最近使っていないのでセットアップが面倒。やはりすぐに使えるLinux環境が必要だな。
やっと特性補正ができるようになってきた。しかしSACの操作には忍耐が必要。広帯域地震計の応答特性補正手順覚え書き。
(1) rdseed option pでseedファイルからpoles
and zerosを抜き出す。SAC_PZs_II_OBN_LHN_00_YYYY.ddd.hh.00.0000...等のファイルが生成される。
(2) sacを起動し地震計データファイルを読み込み、DC成分をカット。
SAC> r *DGAR.00.LHN.Q.*
SAC> rmean
(3) poles and zeroファイルによる応答特性の補正。長周期ノイズカット。テキストファイル保存。(xxxxxxxはpoles
and zerosファイル)
SAC> transfer from polezero s xxxxxx
SAC> hp co 0.003
SAC> w alpha DGAR_LHN
一応特性補正と同時に変位(displacement)に変換される様。ただし特性補正すると大きな長周期ノイズが載るのでハイパスフィルタでこれをカットしないと使えない。STS-1でも固有振動周期360s
(0.003Hz) より低い周波数では感度が落ち、補正をしてもSN比が小さすぎ使えない様だ。さてGPS地震計の超低周波特性の検証はどうすればいいのだろう。
応答特性補正しdeconvolutionした結果(HPF:0.003Hz-
)と単純な時間積分と殆ど差がでないことが分かった
(青:deconv,赤:積分)。むしろdeconvolutionすると変なノイズが混入することがある。結論として応答特性補正をしてもGPSとの一致性は良くならない。苦労したのにガックリくる結論。
.....................................................................................................................................
HR-PPP論文引き続き。やっと形になりつつある。しかし効率悪すぎ。いったい何日かかっているのだろう。いつも思うのだが技術者にしても研究者にしても欧米人と対等に渡り合うには言語のハンデを乗り越えなければならない。
5/31に書いた信号送信時の衛星位置計算の件。ENRI福島さんから丁寧な回答を頂いた。一部誤解があり、解説には少し省略があるがプログラム自体はノバテルであれば問題ないことを確認した。福島さん、お騒がせして申し訳有りませんでした。
.....................................................................................................................................
測位とは関係ない仕事を一つ片づけ。次は測位関係だが内容は書けない件の検討。だんだんとその手の仕事が増えてきた。ところでこれは書いてしまって問題ないと思うので書くが、4月から定期的に東京海洋大安田先生のところで学生さんの指導等の手伝いをしている。人に教えるというのは自分の頭の中が整理されていないと無理なので必然的に理解が深まるし、また新しい知識も色々と得られて大変勉強になる。ホントはちゃんとした数学をもう一度勉強し直したいと思っているのがこれは長期でボチボチとやっていく予定。
.....................................................................................................................................
急に色々とせわしなくなってきた。HR-PPP論文も途中で止まってしまっているのだが内容を忘れないうちにとりあえずの決着をつけなければならない。
.....................................................................................................................................
信号送信時の衛星位置の求め方の別解。精密測位の理論及び解析処理、RTK測位の基礎と実装ではこっちを採用している。
(1) trを受信機時計で計った受信時刻、dtrを受信機時計誤差としてとして幾何学距離ρを以下light-time
eq.を解いて求める。
ρ=| Rz(ωρ/c) rs(tr-dtr-ρ/c)-rr |
(2) dtrは普通単独測位で求めるが、単独測位中で(1)を計算する場合はdtrの初期値を0とおいて単独測位の繰り返し計算中で逐次近似でdtrを求める。
(3) 以上で信号受信時のECEF座標系における信号送信時の衛星位置がRz(ωρ/c) rs(tr-dtr-ρ/c)で求められる。
6/1に書いた解との差は、こちらはlight-time eq.を解く際に衛星位置を再計算しなければならないので計算コストがかかる。疑似距離欠測時や搭載時計切り替え等で放送暦時計が信用できない場合でも解が求まる点はこちらの方が有利。まあどちらでも良い。色々な参考書でこの解を使いながらdtrを無視してしまう間違いを多く見かける。特にAshtecやTrimbleの様なジグザグ時計受信機やGPSTへの同期を行っていない外部時計を使う場合にはdtrの大きさが数100μs以上になるのでこの項は全く無視できない。
上記計算につき5/31に参考書ほぼ全滅と書いたが、Leick 3rd ed.を再度確認したら正しく書いてあった (5.3.2)。ただよほど慎重に追っていかないと間違える書き方で分かりにくい。でもLeickは一応信頼できる参考書と言うことでお勧め。
いつのまにかGoogleページランクが(2/10)に上がっている。長らく(0/10)だったのだけれど。でもページランクって他からリンクされてないと上がらないはずなのだが、どこかリンクが増えたのだろうか。もしかすると検索から飛ぶ回数が増えると上がるのかも知れない。なお本サイトはリンクフリーです。勝手にどんどんリンクを張ってください。
.....................................................................................................................................
HR-PPPから派生して、測位とは何か、座標と何か、絶対/相対値の差はどこにあるか等つらつらと考える。あんまりつっこんで考えすぎると哲学にならざるを得ないのでいい加減なところで保留しておかないといけない。でも頭の中を文章に書き出してみると色々なことが整理されて分かった気分になる。でも本当は全く分かっていないのかもしれない。
Amazonで届いた参考書
安芸, リチャーズ, 地震学 定量的アプローチ,
古今書院, 2004
著名な理論地震学教科書、Aki & Rechards,
Quantitative Seismology 2nd ed.の邦訳。800頁を越える大著。ざっと中を見るとコテコテの数式表現がずっと続いている。地震学と言うとどうも泥臭いイメージが有るが実際には裏付けとなる数学理論が確立されているようだ。調べてみると、大変残念なことに安芸敬一先生は、昨年75歳でお亡くなりになっている様だ。
.....................................................................................................................................
昨日書いた信号送信時の衛星位置の求め方。それじゃ正しい求め方は何なんだとつっこまれそうなので一番分かりやすい解を簡単に書いておく。ちゃんとは別途まとめるつもり。
(1) trを受信機時計で計った受信時刻(RINEXで言えば観測データの先頭に書いてある時刻、オフセットがあればそれも考慮しなければいけない)、Pを疑似距離観測値として、(真の)送信時刻tsは ts=tr-P/c-dT(ts) で求める。dT(t)は時刻tにおける衛星時計誤差で放送暦または精密暦から求める。衛星時計安定度は10-11はあるので衛星時計ドリフトは10-10以下なので (訂正、6/10) dT(ts)の代わりにdT(tr)を使っても問題ない。またTGD/DCBや相対論効果、放送暦時計の誤差も安全に無視できる。(補足: 主に電離層遅延の差でL1, L2信号送信時の衛星位置は厳密には異なるがこの差も1mm未満で無視できる。ただ測位に使う観測値を使うのが妥当。6/1
22:43)
(2) 時刻tにおける衛星(アンテナ位相中心)位置をrs(t)、信号受信時の受信機(アンテナ位相中心)位置をrrとして、幾何学距離ρを以下light-time eq.を解いて求める。
ρ=| Rz(ωρ/c) rs(ts)-rr | 。ここでRzはZ軸周りの座標回転行列, ωは地球自転角速度(rad/s)である。また衛星位置は放送暦または精密暦から求めるが精密暦の場合衛星重心位置なのでアンテナオフセットの補正が必要となる(放送暦は位相中心位置のはずだが実際は少し怪しい)。ここで極運動のため自転軸はZ軸と一致しないがこの効果は1mm以下なので無視している(mm以下では考慮が必要)。また伝搬時間計算時の対流圏/電離層等の影響も安全に無視できる。(補足: 連続的に受信機時計をGPSTに合わせ込むClock
Steering動作をする受信機では電波伝搬時間を疑似距離と衛星時計誤差から求めることも可能だが一般にはlight-time
eq.を解かないと電波伝搬時間を正確に求められない。6/1
23:21)
(3) 以上で信号受信時のECEF座標系における信号送信時の衛星位置がRz(ωρ/c) rs(ts)で求められる。
以上以外の方法は数cm程度以上の近似誤差(または間違い)を含んでいる可能性が高い。なお地球回転をsagnac効果項として幾何学距離とは別に補正する方法もあるが以上の方が理解が容易であるし近似も入らない。また以上の座標系は全部ECEFであるがGTでは慣性系で扱っているためやり方は異なっている。もう一点注意。通常の測位計算では時刻をGPS週+週先頭からの秒数(tow)で表す場合が多いが、この方法だと倍精度でも0.01ns(3mm)以下を正確に表せない。従って時刻の内部表現については桁落ちに対する十分な考慮が必要となる。
以上を書いていて気づいたのだが、通常の単独測位の精度は良くても数mなので正しくない計算をしてもそれほど問題にならない。ただDGPSではこの影響が無視できない。知る限りDGPSで使う単独測位アルゴリズム規格は存在しないので、DGPSの精度悪化は受信機に組み込まれた計算モデルの問題に起因している部分が少なくないのではないか。(もちろんDGPS補正用PRCを作る側で問題があれば話にならないが)
T.Ford et al., GPS/MEMS Inertiial Integration Methodology
and Results, ION 2004
NovAtel OEM4-G2とMEMSベースIMUのGPS/INS統合システムの測位精度評価。IMUとしてはBAE社SiIMU01を使用。10秒GPS欠測後の測位精度悪化が水平0.39m,
垂直0.21mとしている。加速度計の位置精度は時間の2乗で効くはずなので案外性能が良くない。MEMSベースのIMUではバイアスやミスアライメント誤差が大きくなかなか精度が出ない様だ。この論文を含めNovAtel関係技術論文はここから参照できる。しかし凄い量である。
.....................................................................................................................................
| Home | by T.Takasu |